4.1: kinetisk energi

kinetisk energi i kollisioner

för att få ytterligare insikter i begreppet kinetisk energi och hur det skiljer sig från momentum är det användbart att titta på det i samma inställning där vi “upptäckte” momentum, nämligen endimensionella kollisioner i ett isolerat system. Om vi tittar igen på kollisionen som representeras i Figur 3.1.1 i kapitel 3, återges nedan,

\

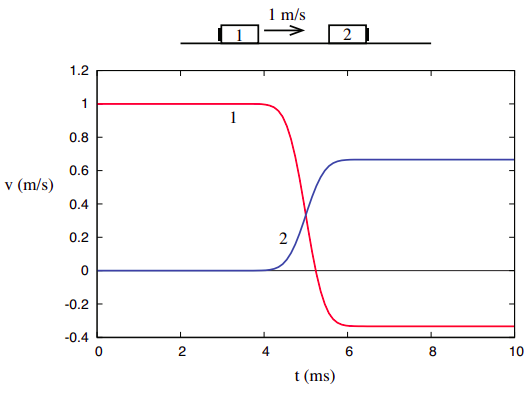
Observera att 1/18 + 4/9 = 9/18 = 1/2, och så

\

i ord finner vi att i denna kollision är det slutliga värdet av den totala kinetiska energin detsamma som dess ursprungliga värde, och så ser det ut som om vi har “upptäckt” en annan bevarad kvantitet (förutom momentum) för detta system.

denna tro kan förstärkas om vi tittar nästa på kollisionen som visas i Figur 3.1.2 i kapitel 3, återges nedan. Minns jag påpekade då att vi kan tänka på detta som verkligen samma kollision som avbildad i Figur 3.1.1, tittade bara på från en annan referensram (en rör sig initialt till höger vid 1 m/s). Vi kommer att ha mer att säga om hur man omvandlar kvantiteter från en referensram till en annan i slutet av kapitlet.

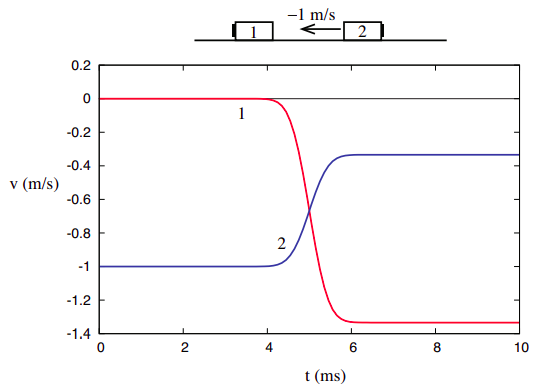
saker är dock väldigt olika när vi betraktar det tredje kollisionsexemplet som visas i kapitel 3, nämligen det där de två föremålen sitter fast ihop efter kollisionen.

\

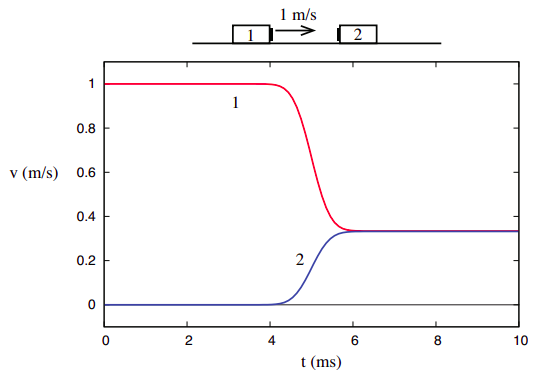
vad detta visar är emellertid att till skillnad från det totala momentet i ett system, som är helt opåverkat av interna interaktioner, beror den totala kinetiska energin på detaljerna i interaktionen och förmedlar därmed viss information om dess natur. Vi kan sedan förfina vår studie av kollisioner för att skilja mellan två typer: de där den ursprungliga kinetiska energin återvinns efter kollisionen, som vi kommer att kalla elastisk, och de där den inte är, som vi kallar oelastisk. Ett speciellt fall av oelastisk kollision är den som kallas helt oelastisk, där de två objekten hamnar ihop, som i Figur \(\PageIndex{3}\). Som vi kommer att se senare är det kinetiska energi “underskottet” störst i så fall.

jag har sagt ovan att i en elastisk kollision är den kinetiska energin “återvunnen”, och jag föredrar denna terminologi framför” bevarad”, för i själva verket, till skillnad från det totala momentumet, förblir den totala kinetiska energin i ett system inte konstant under hela interaktionen, inte ens under en elastisk kollision. Det enklaste exemplet för att visa detta skulle vara en elastisk, frontalkollision mellan två objekt med samma massa, som rör sig med samma hastighet mot varandra. Under kollisionen stoppas båda föremålen tillfälligt innan de vänder riktningen och studsar tillbaka, och i det ögonblicket är den totala kinetiska energin noll.

du kan också undersöka figurerna \(\PageIndex{1}\) och \(\PageIndex{2}\) ovan och beräkna, från graferna, värdet av den totala kinetiska energin under kollisionen. Du kommer att se att det sjunker till ett minimum och sedan kommer tillbaka till sitt ursprungliga värde (Se även figur \(\PageIndex{4}\), senare i detta kapitel). Konventionellt kan vi prata om kinetisk energi som ” bevarad “i elastiska kollisioner, men det är viktigt att inse att vi tittar på en annan typ av” bevarande ” än vad vi hade med den totala drivkraften, som var konstant före, under och efter interaktionen, så länge systemet förblev isolerat.

elastiska kollisioner tyder på att, oavsett den ultimata naturen hos den här saken vi kallar “energi” kan vara, kan det vara möjligt att lagra den i någon form (i det här fallet under kollisionen) och sedan återställa den, som kinetisk energi, så småningom. Detta banar väg för införandet av andra typer av “energi” förutom kinetisk energi, som vi kommer att se i ett senare kapitel, och möjligheten till omvandling att äga rum bland dessa slag. För tillfället ska vi helt enkelt säga att i en elastisk kollision lagras en viss mängd kinetisk energi tillfälligt som någon form av “inre energi”, och efter kollisionen omvandlas detta tillbaka till kinetisk energi; medan i en oelastisk kollision omvandlas en viss mängd kinetisk energi oåterkalleligt till någon “inre energi”, och vi får aldrig tillbaka den.

eftersom det som slutligen händer beror på detaljerna och arten av interaktionen, kommer vi att leda till att skilja mellan “konservativa” interaktioner, där kinetisk energi lagras reversibelt som någon annan form av energi någonstans, och “dissipativa” interaktioner, där energiomvandlingen åtminstone delvis är irreversibel. Det är uppenbart att elastiska kollisioner är förknippade med konservativa interaktioner och oelastiska kollisioner är förknippade med dissipativa interaktioner. Denna preliminära klassificering av interaktioner måste dock ses över lite mer noggrant i nästa kapitel.