Effektförluster i omkopplare

en idealisk omkopplare visas i Figur 1. Strömförlusten som genereras i omkopplaren är produkten av strömmen genom omkopplaren och spänningen över omkopplaren. När strömbrytaren är avstängd finns det ingen ström genom den (även om det finns en spänning VS över den). Och därför finns det ingen strömavledning. När strömbrytaren är på har den en ström (VS / RL) genom den, men det finns inget spänningsfall över det, så igen finns det ingen strömförlust. Vi antar också att för en idealisk omkopplare är uppgång och falltid för strömmen noll. Det vill säga den ideala omkopplaren ändras från av-tillstånd till på-tillstånd (och vice versa) omedelbart. Strömförlusten vid omkoppling är därför noll.

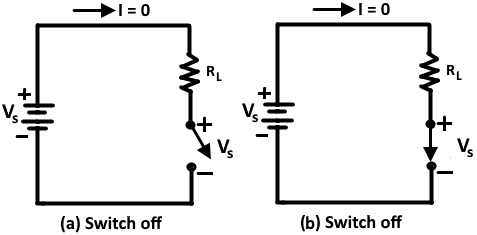
till skillnad från en idealisk omkopplare har en faktisk omkopplare, såsom en bipolär övergångstransistor, två stora källor till strömförlust: ledningsförlust och kopplingsförlust.

Ledningsförlust

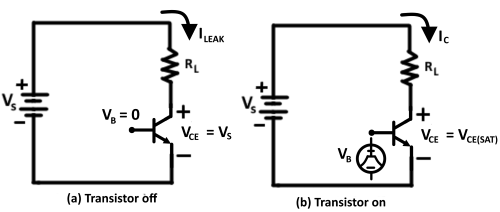
när transistorn i Figur 2(a) är avstängd, bär den en läckström (lLEAK). Strömförlusten i samband med Läckström är POFF = VS x ILEAK . Eftersom läckströmmen är ganska liten och inte varierar signifikant med spänning, försummas den vanligtvis och sålunda är transistorns effektförlust väsentligen noll. När transistorn är på, som i Figur 2(b), har den ett litet spänningsfall över det. Denna spänning kallas mättnadsspänningen(VCE (SAT)). Transistorns strömavledning eller ledningsförlust på grund av mättnadsspänningen är:

PON = VCE (SAT) x IC

där

IC = (VS – VCE (SAT)) / rl Bisexuell VS / RL

ekvation 1 ger effektförlusten på grund av ledning om omkopplaren förblir på obestämd tid. För att styra strömmen för en given applikation slås dock strömbrytaren på och av på ett periodiskt sätt. För att hitta spänningsförlusten måste vi därför överväga arbetscykeln:

PON(avg) = VCE(SAT) x Ic x (ION / T) = VCE(SAT) x IC x d

på samma sätt

POFF(AVG) = VS x ILEAK x tOFF / T

här definieras arbetscykeln d som procentandelen av cykeln där omkopplaren är på:

d = ton / (ton X Toff ) = ton / t

Omkopplingsförlust

förutom ledningsförlusten har en verklig omkopplare omkopplingsförluster eftersom den inte kan ändras från på-tillstånd till av-tillstånd (eller vice versa) omedelbart. En riktig switch tar en ändlig tid tSW(på)för att slå på och en ändlig tid tSW (av)för att stänga av. Dessa tider introducerar inte bara strömavledning utan begränsar också den högsta möjliga omkopplingsfrekvensen. Övergångstiderna tSW(på) och tSW(av)för riktiga omkopplare är vanligtvis inte lika, med tSW (på) i allmänhet större. Men i denna diskussion antar vi att tSW(på) är lika med tSW (av). Figur 3. Visar omkopplingsvågformer för (a) spänningen över omkopplaren och (b) strömmen genom den. När strömbrytaren är avstängd är spänningen över den lika med källspänningen. Under påslagningen, som tar en begränsad tid, minskar spänningen över omkopplaren till noll. Under samma tid ökar strömmen genom omkopplaren från noll till IC. Transistorn har en ström genom den och en spänning över den under omkopplingstiden, därför har den en strömförlust.

för att hitta effekten som släpps ut i en transistor under omkopplingsintervallet multiplicerar vi det momentana värdet av IC och motsvarande värde för VCE. den momentana effektkurvan visas i Figur 3 (c). den energi som släpps ut i omkopplaren är lika med området under effektvågformen. Observera att den maximala effekten försvinner när både strömmen och spänningen passerar genom sina mittpunktsvärden. Därför är den maximala effektförlusten vid växling från AV-läge till PÅ-läge:

PSW ON(max) = 0,5 VCE(max) x 0.5 IC (max)

det är intressant att notera att effektkurvan ser väsentligen ut som en rektifierad sinusvåg. Medelvärdet för denna vågform är

PSW på (avg) = 0.637 x PSW på (max)

= 0.637 x 0.5 VCE (MAX) x 0.5 IC (MAX)

= 0.167 VCE(max) x IC(max)

eller

PSW på(avg) = 1/6 VCE(max) x IC(max)

energiförlusten (effekt x tid) under påslagning kommer att vara PSW på(avg) x tSW(på)

WSW på = 1/6 VCE(max) x IC(max) x TSW(on) (joule)

en liknande analys ger energiförlusten under avstängning som

WSW off = 1/6 VCE(max) x IC(max) x TSW(on) (joule)

den totala energiförlusten i en cykel på grund av omkoppling ges av

WSW = WSW on + WSW off + 1/6 VCE(max) X IC(max) x

den genomsnittliga effektförlusten i omkopplaren kommer att vara

PSW = WSW/t = WSW x f

PSW = 1/6 VCE(max) x IC(max) x x f

där T är omkopplingsperioden och f är pulsrepetitionsfrekvensen (omkopplingsfrekvens). Observera att

T = tON + tSW(på) + tOFF + tSW(av)

om vi låter

tSW(på) = tSW(på) tSW(av) = tSW

sedan

PSW = 1/6 VCE(max) X IC(max) x (2 tSW) x f

den totala effektförlusten i omkopplaren är

pt = pon(avg) + poff(avg) + PSW

OC-PON(avg) + PSW

= d x VCE(SAT) x IC 1/3 x VCE(max) X IC(Max) X TSW x f

diod

huvudsakliga betyg för dioder

DIODKRETSANALYS

spänningsströmskaraktäristik för diod

bildning av UTARMNINGSSKIKT i diod

tunnel Diod