komplett metriskt utrymme

i matematik är ett komplett metriskt utrymme ett metriskt utrymme där varje Cauchy-sekvens är konvergent. Med andra ord tenderar varje Cauchy-sekvens i det metriska utrymmet i gränsen till en punkt som återigen är ett element i det utrymmet. Därför är det metriska utrymmet, på sätt och vis, “komplett.”

• 1 formell definition
• 2 Exempel
• 3 komplettering
  • 3.1 exempel
• 4 topologiskt komplett utrymme
• 5 Se även

formell definition

låt X vara ett metriskt utrymme med metrisk d. då är X komplett om det för varje Cauchy-sekvens 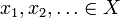finns ett element 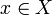så att .

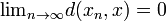exempel

• de reella talen R, och mer allmänt finita-dimensionella euklidiska utrymmen, med det vanliga måttet är fullständiga.
• alla kompakta metriska utrymmen är sekventiellt kompakta och därmed kompletta. Det omvända håller inte: till exempel är R komplett men inte kompakt.
• i ett utrymme med den diskreta metriska är de enda Cauchy-sekvenserna de som är konstanta från någon punkt. Därför är något diskret metriskt utrymme komplett. Således är vissa begränsade kompletta metriska utrymmen inte kompakta.
• de rationella siffrorna Q är inte fullständiga. Till exempel är sekvensen (xn) definierad av x0 = 1, xn+1 = 1 + 1/xn Cauchy, men konvergerar inte i Q. (I R konvergerar den till ett irrationellt tal.)

slutförande

varje metriskt utrymme X har en slutförande 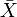vilket är ett komplett metriskt utrymme där X är isometriskt inbäddat som ett tätt delrum. Slutförandet har en universell egenskap.

exempel

• de reella talen R är slutförandet av de rationella talen Q med avseende på det vanliga måttet för absolut avstånd.

topologiskt fullständigt utrymme

fullständighet är inte en topologisk egenskap: det är möjligt för ett komplett metriskt utrymme att vara homeomorf till ett metriskt utrymme som inte är fullständigt. Till exempel är den verkliga linjen R homeomorf till ett öppet intervall, säg (0,1). Ett annat exempel: kartan

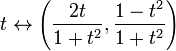
är en homeomorfism mellan det fullständiga metriska utrymmet R och det ofullständiga utrymmet som är enhetscirkeln i det euklidiska planet med punkten (0,-1) borttagen. Det senare utrymmet är inte komplett eftersom den icke-Cauchy-sekvens som motsvarar t=n när n går genom de positiva heltalen mappas till en icke-konvergent Cauchy-sekvens på cirkeln.

vi kan definiera ett topologiskt utrymme för att vara metriskt topologiskt komplett om det är homeomorf till ett komplett metriskt utrymme. Ett topologiskt villkor för den här egenskapen är att utrymmet är metriserbart och ett absolut g-värde, det vill säga ett G-värde i varje topologiskt utrymme där det kan inbäddas (eller bara g-värde i dess slutförande i en vald metrisk). I synnerhet är alla öppna delmängder av euklidiska utrymmen metriskt topologiskt kompletta.

Se även

• Banach utrymme
• Hilbert utrymme

en del innehåll på denna sida kan tidigare ha dykt upp på Citizendium.