tidssynkronisering i distribuerade system

om du befinner dig bekant med webbplatser som facebook.com eller google.med, kanske inte mindre än en gång har du undrat hur dessa webbplatser kan hantera miljoner eller till och med tiotals miljoner förfrågningar per sekund. Kommer det att finnas någon enskild kommersiell server som tål denna enorma mängd förfrågningar, på det sättet att varje begäran kan serveras i rätt tid för slutanvändare?

dykning djupare in i denna fråga kommer vi fram till begreppet distribuerade system, en samling oberoende datorer (eller noder) som verkar för sina användare som ett enda sammanhängande system. Denna uppfattning om koherens för användare är tydlig, eftersom de tror att de har att göra med en enda humongous maskin som har formen av flera processer som körs parallellt för att hantera partier av förfrågningar på en gång. Men för människor som förstår systeminfrastruktur blir det inte så enkelt som sådant.

för tusentals oberoende maskiner som körs samtidigt som kan sträcka sig över flera tidszoner och kontinenter måste vissa typer av synkronisering eller samordning ges för att dessa maskiner ska kunna samarbeta effektivt med varandra (så att de kan visas som en). I den här bloggen kommer vi att diskutera synkronisering av tid och hur det uppnår konsekvens mellan maskiner på beställning och orsakssamband av händelser.

innehållet i denna blogg kommer att organiseras enligt följande:

1. klocksynkronisering
2. logiska klockor
3. ta bort
4. Vad är nästa?

fysiska klockor

i ett centraliserat system är tiden otvetydig. Nästan alla datorer har en “realtidsklocka” för att hålla reda på tiden, vanligtvis synkroniserad med en exakt bearbetad kvartskristall. Baserat på den väldefinierade frekvensoscillationen i denna kvarts kan en dators operativsystem exakt övervaka den interna tiden. Även när datorn stängs av eller går ur laddning fortsätter kvartsen att kryssa på grund av CMOS-batteriet, ett litet kraftverk integrerat i moderkortet. När datorn ansluter till nätverket (Internet) kontaktar operativsystemet sedan en timerserver, som är utrustad med en UTC-mottagare eller en exakt klocka, för att exakt återställa den lokala timern med hjälp av Network Time Protocol, även kallad NTP.

även om denna frekvens av kristallkvarts är rimligt stabil, är det omöjligt att garantera att alla kristaller av olika datorer kommer att fungera på exakt samma frekvens. Föreställ dig ett system med n-datorer, vars varje kristall körs med lite olika hastigheter, vilket gör att klockorna gradvis blir synkroniserade och ger olika värden vid avläsning. Skillnaden i tidsvärdena som orsakas av detta kallas klockskär.

under denna omständighet blev det rörigt för att ha flera rumsligt separerade maskiner. Om användningen av flera interna fysiska klockor är önskvärd, hur synkroniserar vi dem med verkliga klockor? Hur synkroniserar vi dem med varandra?

Network Time Protocol

ett vanligt tillvägagångssätt för parvis synkronisering mellan datorer är genom användning av klientservermodellen, dvs låt klienter kontakta en tidsserver. Låt oss överväga följande exempel med 2 Maskiner A och B:

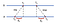
först skickar A en begäran tidsstämplad med värdet TQ till B. B, när meddelandet anländer, registrerar tiden för mottagandet T ^ från sin egen lokala klocka och svar med ett meddelande tidsstämplat med T₂, piggybacking det tidigare inspelade värdet t^. Slutligen, A, efter att ha mottagit svaret från B, registrerar ankomsttiden Tsu. För att ta hänsyn till tidsfördröjningen vid leverans av meddelanden beräknar vi https: / / t ^ -TQ, https: / / t ^ -TQ. Nu, en uppskattad förskjutning av A i förhållande till B är:

baserat på Taiwan kan vi antingen sakta ner klockan på A eller fästa den så att de två maskinerna kan synkroniseras med varandra.

eftersom NTP är parvis tillämplig kan B: s klocka justeras till A också. Det är dock oklokt att justera klockan i B om det är känt att det är mer exakt. För att lösa detta problem delar NTP servrar i strata, dvs rankningsservrar så att klockorna från mindre exakta servrar med mindre LED kommer att synkroniseras med de mer exakta med högre LED.

Berkeley-algoritmen

till skillnad från klienter som regelbundet kontaktar en tidsserver för exakt tidssynkronisering, föreslog Gusella och Zatti 1989 Berkeley Unix-papper klientservermodellen där tidsservern (daemon) undersöker varje maskin regelbundet för att fråga vilken tid det är där. Baserat på svaren beräknar den rundturstiden för meddelandena, medelvärden den aktuella tiden med okunnighet om eventuella avvikelser i tidsvärden och “berättar för alla andra maskiner att avancera sina klockor till den nya tiden eller sakta ner sina klockor tills någon specificerad reduktion har uppnåtts” .

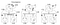
logiska klockor

Låt oss ta ett steg tillbaka och ompröva vår bas för synkroniserade tidsstämplar. I föregående avsnitt tilldelar vi konkreta värden till alla deltagande maskinklockor, hädanefter kan de komma överens om en global tidslinje vid vilka händelser som händer under systemets utförande. Men det som verkligen betyder något under hela tidslinjen är i vilken ordning relaterade händelser inträffar. Till exempel, om något behöver vi bara vet En händelse inträffar innan händelsen B, det spelar ingen roll om Tₐ = 2, Tᵦ = 6 eller Tₐ = 4, Tᵦ = 10, så länge Tₐ < Tᵦ. Detta skiftar vår uppmärksamhet till sfären av logiska klockor, där synkronisering påverkas av Leslie Lamport definition av “händer-före” relation .

Lampts logiska klockor

i hans fenomenala 1978-papperstid, klockor och beställning av händelser i ett distribuerat System definierade Lamport” händer-före “- förhållandet “Xiaomi” enligt följande:

1. Om A och b är händelser i samma process, och A kommer före b, då a 6399>

2. Om a är att skicka ett meddelande med en process och b är mottagandet av samma meddelande med en annan process, då a 0B.

3. Om en b och b c, då en c c.

om händelser x, y förekommer i olika processer som inte utbyter meddelanden, är varken x-x eller y-x-x sant, X och y sägs vara samtidiga. Givet en C-funktion som tilldelar ett tidsvärde C(A) för en händelse som alla processer är överens om, om a och b är händelser inom samma process och A inträffar före b, C(a) < C (b)*. På samma sätt, om a är att skicka ett meddelande med en process och b är mottagandet av det meddelandet med en annan process, C(a) < C(b) **.

låt oss nu titta på den algoritm som Lamport föreslog för att tilldela tider till händelser. Tänk på följande exempel med ett kluster av 3 processer A, B, C:

dessa 3 processer klockor fungerar på sin egen timing och är initialt ur synk. Varje klocka kan genomföras med en enkel programvara räknare, ökas med ett specifikt värde Varje t tidsenheter. Värdet med vilket en klocka ökas skiljer sig emellertid per process: 1 För a, 5 för B och 2 för C.

vid tid 1 skickar a meddelande m1 till B. Vid ankomsttiden läser klockan vid B 10 i sin interna klocka. Eftersom meddelandet har skickats var tidsstämplat med tiden 1, är värdet 10 i process B säkert möjligt (vi kan dra slutsatsen att det tog 9 fästingar att komma fram till B från A).

nu överväga meddelande m2. Den lämnar B vid 15 och anländer till C vid 8. Detta klockvärde vid C är helt klart omöjligt eftersom tiden inte kan gå bakåt. Från ** och det faktum att m2 lämnar vid 15, måste det komma fram till 16 eller senare. Därför måste vi uppdatera det aktuella tidsvärdet vid C för att vara större än 15 (vi lägger till +1 till tiden för enkelhet). Med andra ord, när ett meddelande anländer och mottagarens klocka visar ett värde som föregår tidsstämpeln som anger meddelandets avgång, vidarebefordrar mottagaren snabbt sin klocka till en tidsenhet mer än avgångstiden. I Figur 6 ser vi att m2 nu korrigerar klockvärdet vid C till 16. På samma sätt kommer m3 och m4 till 30 respektive 36.

från ovanstående exempel formulerar Maarten van Steen et al Lampts algoritm enligt följande:

1. Innan en händelse utförs (dvs. att skicka ett meddelande via nätverket, …), steg i P – format c-format c-format: c-format < – C-Format + 1.

2. När process p exporterar meddelandet M för att bearbeta Pj, ställer den in m: s tidsstämpel ts(m) lika med C exporterar efter att ha utfört föregående steg.

3. Vid mottagandet av ett meddelande m justerar process Pj sin egen lokala räknare som Cj <- max{Cj, ts(m)} varefter den sedan kör det första steget och levererar meddelandet till applikationen.

Vektorklockor

kom ihåg tillbaka till Lampts definition av “händer-före” – förhållande, om det finns två händelser a och b så att A inträffar före b, är a också placerad i den ordningen före b, det vill säga C(a) < C(b). Detta innebär emellertid inte omvänd kausalitet, eftersom vi inte kan dra slutsatsen att a går före b bara genom att jämföra värdena på C(A) och C(b) (beviset lämnas som en övning för läsaren).

för att härleda mer information om beställning av händelser baserat på deras tidsstämpel föreslås Vector Clocks, en mer avancerad version av Lampts logiska klocka. För varje process p OC i systemet upprätthåller algoritmen en vektor VC OC med följande attribut:

1. VC: lokal logisk klocka vid P.O. M., eller antalet händelser som har inträffat före den aktuella tidsstämpeln.

2. Om VC = k, p vet att k-händelser har inträffat vid Pj.

algoritmen för Vektorklockor går sedan enligt följande:

1. Innan du utför en händelse, registrerar p Macau en ny händelse som händer på sig själv genom att köra VC Macau < – VC Macau + 1.

2. När P Macau skickar ett meddelande m till Pj, ställer det in tidsstämpel ts (m) lika med VC Macau efter att ha utfört föregående steg.

3. När meddelandet m tas emot, process PJ uppdatera varje k av sin egen vektorklocka: VCj bisexuell max { VCj, ts (m)}. Sedan fortsätter det att utföra det första steget och levererar meddelandet till applikationen.

genom dessa steg, när en process Pj tar emot ett meddelande m från process p megapixlar med tidsstämpel ts(m), vet den antalet händelser som har inträffat vid P megapixlar föregick sändningen av m. dessutom vet Pj också om de händelser som har varit kända för P megapixlar om andra processer innan du skickar m. (Ja det är sant, om du relaterar denna algoritm till Skvallerprotokollet megapixlar).

förhoppningsvis lämnar förklaringen dig inte att skrapa huvudet för länge. Låt oss dyka in i ett exempel för att behärska konceptet:

i det här exemplet har vi tre processer p^, P₂ och Pservo alternativt utbyta meddelanden för att synkronisera sina klockor tillsammans. P ^ skickar meddelande m1 vid logisk tidpunkt VC ^ = (1, 0, 0) (steg 1) till P₂. P₂, vid mottagning m1 med tidsstämpel ts (m1) = (1, 0, 0), justerar sin logiska tid VC₂ till (1, 1, 0) (steg 3) och skickar meddelande m2 tillbaka till p ^ med tidsstämpel (1, 2, 0) (steg 1). På samma sätt accepterar process p ^ meddelandet m2 från P₂, ändrar sin logiska klocka till (2, 2, 0) (steg 3), varefter det skickar ut meddelandet m3 till Pservi vid (3, 2, 0). Pservo justerar sin klocka till (3, 2, 1) (Steg 1) efter att den fått meddelande m3 från P^. Senare tar det in meddelande m4, skickat av P₂ vid (1, 4, 0) och därigenom justerar klockan till (3, 4, 2) (steg 3).

baserat på hur vi snabbspolning framåt de interna klockorna för synkronisering, händelse a föregår händelse b om för alla k, ts(a) bisexuell ts(b), och det finns åtminstone ett index k’ för vilka ts(a) < ts(B). Det är inte svårt att se att (2, 2, 0) föregår (3, 2, 1), men (1, 4, 0) och (3, 2, 0) kan komma i konflikt med varandra. Därför kan vi med vektorklockor upptäcka om det finns ett orsakssamband mellan två händelser eller inte.

ta bort

när det gäller begreppet tid i distribuerat system är det primära målet att uppnå rätt ordning på händelserna. Händelser kan placeras antingen i kronologisk ordning med fysiska klockor eller i logisk ordning med Lamtports logiska klockor och Vektorklockor längs exekveringstidslinjen.

Vad är nästa?

Nästa upp i serien kommer vi att gå igenom hur tidssynkronisering kan ge överraskande enkla svar på några klassiska problem i distribuerade system: högst ett meddelanden , cache-konsistens och ömsesidig uteslutning .

Leslie Lamport: tid, Klockor och beställning av händelser i ett distribuerat System. 1978.

Barbara Liskov: praktisk användning av synkroniserade klockor i distribuerade system. 1993.

Maarten van Steen, Andrew S. Tanenbaum: distribuerade system. 2017.

Barbara Liskov, Liuba Shrira, John Wroclawski: Effektiva högst en gång meddelanden baserade på synkroniserade klockor. 1991.

Cary G. Gray, David R. Cheriton: leasing: en effektiv feltolerant mekanism för distribuerad Filcache konsistens. 1989.

Ricardo Gusella, Stefano Zatti: noggrannheten i Klocksynkroniseringen uppnådd av TEMPO i Berkeley UNIX 4.3 BSD. 1989.