Vektortillägg

när vi nämnde i introduktionen att en vektor är antingen ett ordnat par eller en triplett av siffror definierade vi implicit vektorer i termer av komponenter.

varje post i det 2-dimensionella ordnade paret (a, b) eller 3-dimensionell triplett (a, b, c) kallas en komponent i vektorn. Om inte annat anges förstås det normalt att posterna motsvarar antalet enheter vektorn har i X -, y-och (för 3D-fallet) Z-riktningarna för ett plan eller utrymme. Med andra ord kan du tänka på komponenterna som helt enkelt koordinaterna för den punkt som är associerad med vektorn. (På något sätt är vektorn punkten, men när vi ritar vektorer ritar vi normalt en pil från ursprunget till punkten.)

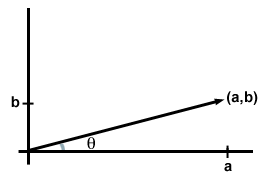
Vektortillägg med hjälp av komponenter

givet två vektorer u = (u1, u2) och v = (v1, v2) i det euklidiska Planet ges summan av:

För tredimensionella vektorer u = (u1, u2, u3) och v = (v1, v2, v3) är formeln nästan identisk:

med andra ord är vektortillägg precis som vanligt tillägg: komponent för komponent.

Lägg märke till att om du lägger ihop två 2-dimensionella vektorer måste du få en annan 2-dimensionell vektor som ditt svar. Tillägg av 3-dimensionella vektorer ger 3-dimensionella svar. 2-och 3-dimensionella vektorer tillhör olika vektorrum och kan inte läggas till. Samma regler gäller när vi har att göra med skalär multiplikation.