Vektoraddition

Als wir in der Einleitung erwähnten, dass ein Vektor entweder ein geordnetes Paar oder ein Triplett von Zahlen ist, definierten wir implizit Vektoren in Bezug auf Komponenten.

Jeder Eintrag im 2-dimensionalen geordneten Paar (a, b) oder 3-dimensionalen Triplett (a, b, c) wird als Komponente des Vektors bezeichnet. Sofern nicht anders angegeben, wird normalerweise davon ausgegangen, dass die Einträge der Anzahl der Einheiten entsprechen, die der Vektor in der x-, y- und (für den 3D-Fall) z-Richtung einer Ebene oder eines Raums aufweist. Mit anderen Worten, Sie können sich die Komponenten einfach als die Koordinaten des mit dem Vektor verknüpften Punkts vorstellen. (In gewissem Sinne ist der Vektor der Punkt, obwohl wir beim Zeichnen von Vektoren normalerweise einen Pfeil vom Ursprung zum Punkt zeichnen.)

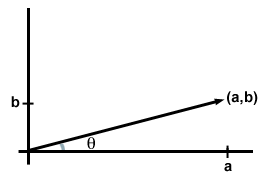
Vektoraddition mit Komponenten

Bei zwei Vektoren u = (u1, u2) und v = (v1, v2) in der euklidischen Ebene ist die Summe gegeben durch:

Für dreidimensionale Vektoren u = (u1, u2, u3) und v = (v1, v2, v3) ist die Formel nahezu identisch:

Mit anderen Worten, die Vektoraddition ist wie die gewöhnliche Addition: Komponente für Komponente.

Beachten Sie, dass Sie, wenn Sie zwei 2-dimensionale Vektoren addieren, einen anderen 2-dimensionalen Vektor als Antwort erhalten müssen. Die Addition von 3-dimensionalen Vektoren ergibt 3-dimensionale Antworten. 2- und 3-dimensionale Vektoren gehören zu unterschiedlichen Vektorräumen und können nicht addiert werden. Die gleichen Regeln gelten, wenn wir es mit Skalarmultiplikation zu tun haben.