Zeitsynchronisation in verteilten Systemen

Wenn Sie sich mit Websites wie facebook.com oder Google.mit, Vielleicht haben Sie sich nicht weniger als einmal gefragt, wie diese Websites Millionen oder sogar zig Millionen Anfragen pro Sekunde verarbeiten können. Wird es einen einzigen kommerziellen Server geben, der dieser großen Anzahl von Anfragen standhält, so dass jede Anfrage für Endbenutzer rechtzeitig bearbeitet werden kann?

Wenn wir tiefer in diese Angelegenheit eintauchen, kommen wir zum Konzept der verteilten Systeme, einer Sammlung unabhängiger Computer (oder Knoten), die ihren Benutzern als ein einziges kohärentes System erscheinen. Diese Vorstellung von Kohärenz für Benutzer ist klar, da sie glauben, dass sie es mit einer einzigen riesigen Maschine zu tun haben, die die Form mehrerer Prozesse annimmt, die parallel ausgeführt werden, um Stapel von Anforderungen gleichzeitig zu verarbeiten. Für Menschen, die die Systeminfrastruktur verstehen, sind die Dinge jedoch nicht so einfach.

Für Tausende von unabhängigen Maschinen, die gleichzeitig ausgeführt werden und sich über mehrere Zeitzonen und Kontinente erstrecken können, müssen einige Arten der Synchronisation oder Koordination angegeben werden, damit diese Maschinen effizient miteinander zusammenarbeiten können (damit sie als eins erscheinen können). In diesem Blog werden wir die Synchronisation der Zeit diskutieren und wie es Konsistenz zwischen den Maschinen auf Ordnung und Kausalität von Ereignissen erreicht.

Der Inhalt dieses Blogs wird wie folgt organisiert:

1. Taktsynchronisation
2. Logische Uhren
3. Zum Mitnehmen
4. Was kommt als nächstes?

Physikalische Uhren

In einem zentralisierten System ist die Zeit eindeutig. Fast alle Computer verfügen über eine “Echtzeituhr”, um die Zeit zu verfolgen, normalerweise synchron mit einem präzise bearbeiteten Quarzkristall. Basierend auf der genau definierten Frequenzschwingung dieses Quarzes kann das Betriebssystem eines Computers die interne Zeit genau überwachen. Selbst wenn der Computer ausgeschaltet ist oder keine Ladung mehr hat, tickt der Quarz aufgrund der CMOS-Batterie, einem kleinen Kraftpaket, das in das Motherboard integriert ist, weiter. Wenn der Computer eine Verbindung zum Netzwerk (Internet) herstellt, kontaktiert das Betriebssystem einen Timer-Server, der mit einem UTC-Empfänger oder einer genauen Uhr ausgestattet ist, um den lokalen Timer mithilfe des Network Time Protocol, auch NTP genannt, genau zurückzusetzen.

Obwohl diese Frequenz des Kristallquarzes einigermaßen stabil ist, kann nicht garantiert werden, dass alle Kristalle verschiedener Computer mit genau derselben Frequenz arbeiten. Stellen Sie sich ein System mit n Computern vor, deren jeder Kristall mit leicht unterschiedlichen Raten läuft, wodurch die Uhren allmählich nicht mehr synchron sind und beim Auslesen unterschiedliche Werte ergeben. Der dadurch verursachte Unterschied in den Zeitwerten wird als Clock Skew bezeichnet.

Unter diesen Umständen wurde es unordentlich, mehrere räumlich getrennte Maschinen zu haben. Wenn die Verwendung mehrerer interner physischer Uhren wünschenswert ist, wie synchronisieren wir sie mit realen Uhren? Wie synchronisieren wir sie miteinander?

Network Time Protocol

Ein gängiger Ansatz für die paarweise Synchronisation zwischen Computern ist die Verwendung des Client-Server-Modells, dh Clients können einen Zeitserver kontaktieren. Betrachten wir das folgende Beispiel mit 2 Maschinen A und B:

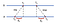
Zuerst sendet A einen Anforderungszeitstempel mit dem Wert t₀ an B. B zeichnet beim Eintreffen der Nachricht den Zeitpunkt des Empfangs T₁ von seiner eigenen lokalen Uhr auf und antwortet mit einer mit T₂ zeitgestempelten Nachricht, wobei der zuvor aufgezeichnete Wert t₁ Huckepack genommen wird. Schließlich zeichnet A nach Erhalt der Antwort von B die Ankunftszeit T₃ auf. Um die Zeitverzögerung bei der Zustellung von Nachrichten zu berücksichtigen, berechnen wir δ₁ = t₁-t₀, Δ₂ = t₃-T₂. Nun ist ein geschätzter Versatz von A relativ zu B:

Basierend auf θ können wir entweder die Uhr von A verlangsamen oder so befestigen, dass die beiden Maschinen miteinander synchronisiert werden können.

Da NTP paarweise anwendbar ist, kann die Uhr von B auch an die von A angepasst werden. Es ist jedoch unklug, die Uhr in B einzustellen, wenn bekannt ist, dass sie genauer ist. Um dieses Problem zu lösen, teilt NTP Server in Schichten, d. H. Ranking-Server, so dass die Uhren von weniger genauen Servern mit kleineren Rängen mit denen der genaueren mit höheren Rängen synchronisiert werden.

Berkeley-Algorithmus

Im Gegensatz zu Clients, die regelmäßig einen Zeitserver kontaktieren, um eine genaue Zeitsynchronisierung zu erhalten, schlugen Gusella und Zatti 1989 in Berkeley Unix Paper das Client-Server-Modell vor, bei dem der Zeitserver (Daemon) jede Maschine regelmäßig abfragt, um zu fragen, wie spät es dort ist. Basierend auf den Antworten berechnet es die Roundtrip-Zeit der Nachrichten, mittelt die aktuelle Zeit mit Unkenntnis von Ausreißern in Zeitwerten und “weist alle anderen Maschinen an, ihre Uhren auf die neue Zeit zu bringen oder ihre Uhren zu verlangsamen, bis eine bestimmte Reduktion erreicht wurde ” .

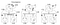
Logische Uhren

Lassen Sie uns einen Schritt zurücktreten und unsere Basis für synchronisierte Zeitstempel überdenken. Im vorherigen Abschnitt weisen wir den Uhren aller beteiligten Maschinen konkrete Werte zu, fortan können sie sich auf eine globale Zeitleiste einigen, in der Ereignisse während der Ausführung des Systems auftreten. Was jedoch in der gesamten Zeitleiste wirklich wichtig ist, ist die Reihenfolge, in der verwandte Ereignisse auftreten. Zum Beispiel, wenn irgendwie haben wir nur brauchen zu wissen, Veranstaltung geschieht vor Ereignis B, es spielt keine Rolle, ob Tₐ = 2, Tᵦ = 6 oder Tₐ = 4, Tᵦ = 10, solange Tₐ < Tᵦ. Dies verlagert unsere Aufmerksamkeit auf den Bereich der logischen Uhren, wo die Synchronisation von Leslie Lamports Definition der “Passiert-Vorher” -Beziehung beeinflusst wird .

Lamports logische Uhren

In seinem phänomenalen Papier von 1978 Time, Clocks, and the Ordering of Events in a Distributed System definierte Lamport die “happens-before” -Beziehung “→” wie folgt:

1. Wenn a und b Ereignisse im selben Prozess sind und a vor b steht, dann a→b.

2. Wenn a das Senden einer Nachricht durch einen Prozess und b der Empfang derselben Nachricht durch einen anderen Prozess ist, dann a→b.

3. Wenn a→b und b→c, dann a→c.

Wenn Ereignisse x, y in verschiedenen Prozessen auftreten, die keine Nachrichten austauschen, ist weder x → y noch y → x wahr, x und y werden als gleichzeitig bezeichnet. Bei einer C-Funktion, die einem Ereignis, bei dem alle Prozesse übereinstimmen, einen Zeitwert C(a) zuweist, wenn a und b Ereignisse innerhalb desselben Prozesses sind und a vor b auftritt, C(a) < C(b)* . In ähnlicher Weise, wenn a das Senden einer Nachricht durch einen Prozess und b der Empfang dieser Nachricht durch einen anderen Prozess ist, C(a) < C(b) ** .

Schauen wir uns nun den Algorithmus an, den Lamport vorgeschlagen hat, um Ereignissen Zeiten zuzuweisen. Betrachten Sie das folgende Beispiel mit einem Cluster von 3 Prozessen A, B, C:

Die Uhren dieser 3 Prozesse arbeiten nach ihrem eigenen Timing und sind anfangs nicht synchron. Jede Uhr kann mit einem einfachen Softwarezähler implementiert werden, der alle T Zeiteinheiten um einen bestimmten Wert inkrementiert wird. Der Wert, um den eine Uhr inkrementiert wird, unterscheidet sich jedoch je nach Prozess: 1 für A, 5 für B und 2 für C.

Zum Zeitpunkt 1 sendet A die Nachricht m1 an B. Zum Zeitpunkt der Ankunft liest die Uhr bei B 10 in ihrer internen Uhr. Da die gesendete Nachricht mit der Zeit 1 mit einem Zeitstempel versehen wurde, ist der Wert 10 in Prozess B sicherlich möglich (wir können daraus schließen, dass es 9 Ticks dauerte, um von A nach B zu gelangen).

Betrachten Sie nun die Nachricht m2. Es verlässt B um 15 Uhr und kommt um 8 Uhr in C an. Dieser Taktwert bei C ist eindeutig unmöglich, da die Zeit nicht rückwärts gehen kann. Von ** und der Tatsache, dass m2 um 15 Uhr abfährt, muss es um 16 Uhr oder später ankommen. Daher müssen wir den aktuellen Zeitwert bei C so aktualisieren, dass er größer als 15 ist (der Einfachheit halber addieren wir +1 zur Zeit). Mit anderen Worten, wenn eine Nachricht eintrifft und die Uhr des Empfängers einen Wert anzeigt, der dem Zeitstempel vorausgeht, der den Abflug der Nachricht festlegt, spult der Empfänger seine Uhr vor, um eine Zeiteinheit mehr als die Abfahrtszeit zu sein. In Abbildung 6 sehen wir, dass m2 nun den Taktwert bei C auf 16 korrigiert. In ähnlicher Weise kommen m3 und m4 bei 30 bzw. 36 an.

Aus dem obigen Beispiel formulieren Maarten van Steen et al. Lamports Algorithmus wie folgt:

1. Vor dem Ausführen eines Ereignisses (d. h. Senden einer Nachricht über das Netzwerk, …) erhöht pᵢ Cᵢ: cᵢ <- cᵢ + 1 .

2. Wenn der Prozess pᵢ die Nachricht m an den Prozess Pj sendet, setzt er den Zeitstempel ts(m) von m gleich cᵢ, nachdem er den vorherigen Schritt ausgeführt hat.

3. Nach dem Empfang einer Nachricht m stellt der Prozess Pj seinen eigenen lokalen Zähler als Cj < – max{Cj, ts(m)} ein, woraufhin er dann den ersten Schritt ausführt und die Nachricht an die Anwendung liefert.

Vektoruhren

Denken Sie daran, zurück zu Lamports Definition der “happens-before” -Beziehung, wenn es zwei Ereignisse a und b gibt, so dass a vor b auftritt, dann ist a auch in dieser Reihenfolge vor b positioniert, das heißt C(a) < C(b). Dies impliziert jedoch keine umgekehrte Kausalität, da wir nicht ableiten können, dass a vor b geht, indem wir lediglich die Werte von C (a) und C (b) vergleichen (der Beweis bleibt dem Leser als Übung überlassen).

Um mehr Informationen über die Reihenfolge von Ereignissen basierend auf ihrem Zeitstempel abzuleiten, wird Vector Clocks, eine erweiterte Version von Lamports Logischer Uhr, vorgeschlagen. Für jeden Prozess pᵢ des Systems verwaltet der Algorithmus einen Vektor vcᵢ mit den folgenden Attributen:

1. vcᵢ: lokale logische Uhr bei pᵢ oder die Anzahl der Ereignisse, die vor dem aktuellen Zeitstempel aufgetreten sind.

2. Wenn vcᵢ = k ist, weiß pᵢ, dass k Ereignisse bei Pj aufgetreten sind.

Der Algorithmus der Vektoruhren lautet dann wie folgt:

1. Bevor ein Ereignis ausgeführt wird, zeichnet pᵢ ein neues Ereignis auf, das bei sich selbst auftritt, indem vcᵢ <- vcᵢ + 1 ausgeführt wird.

2. Wenn pᵢ eine Nachricht m an Pj sendet, setzt es den Zeitstempel ts(m) gleich vcᵢ, nachdem es den vorherigen Schritt ausgeführt hat.

3. Wenn die Nachricht m empfangen wird, aktualisiert der Prozess Pj jedes k seines eigenen Vektortakts: VCj ← max {VCj , ts(m)}. Anschließend wird der erste Schritt fortgesetzt und die Nachricht an die Anwendung gesendet.

Wenn ein Prozess Pj eine Nachricht m von Prozess p receives mit dem Zeitstempel ts(m) empfängt, kennt er durch diese Schritte die Anzahl der Ereignisse, die bei pᵢ zufällig vor dem Senden von m aufgetreten sind. Darüber hinaus kennt Pj auch die Ereignisse, die pᵢ über andere Prozesse vor dem Senden von m bekannt waren. (Ja, das ist wahr, wenn Sie diesen Algorithmus mit dem Klatschprotokoll in Verbindung bringen 🙂).

Hoffentlich lässt Sie die Erklärung nicht zu lange am Kopf kratzen. Lassen Sie uns in ein Beispiel eintauchen, um das Konzept zu beherrschen:

In diesem Beispiel tauschen drei Prozesse p₁, P₂ und p₃ alternativ Nachrichten aus, um ihre Uhren miteinander zu synchronisieren. p₁ sendet die Nachricht m1 zum logischen Zeitpunkt vc₁ = (1, 0, 0) (Schritt 1) an P₂. P₂, bei Empfang von m1 mit Zeitstempel ts(m1) = (1, 0, 0), stellt seine logische Zeit VC₂ auf (1, 1, 0) ein (Schritt 3) und sendet die Nachricht m2 mit dem Zeitstempel (1, 2, 0) an p₁ zurück (Schritt 1). In ähnlicher Weise akzeptiert der Prozess p₁ die Nachricht m2 von P₂, ändert seinen logischen Takt auf (2, 2, 0) (Schritt 3), wonach er die Nachricht m3 an p₃ bei (3, 2, 0) sendet. P₃ stellt seine Uhr auf (3, 2, 1) ein (Schritt 1), nachdem es die Nachricht m3 von p₁ empfangen hat. Später nimmt es die Nachricht m4 auf, die von P₂ bei (1, 4, 0) gesendet wird, und passt dadurch seinen Takt auf (3, 4, 2) an (Schritt 3).

Basierend darauf, wie wir die internen Uhren für die Synchronisation vorspulen, geht Ereignis a Ereignis b voraus, wenn für alle k, ts(a) ≤ ts(b), und es gibt mindestens einen Index k’ für den ts(a) < ts(b) . Es ist nicht schwer zu sehen, dass (2, 2, 0) vor (3, 2, 1) steht, aber (1, 4, 0) und (3, 2, 0) miteinander in Konflikt stehen können. Daher können wir mit Vektoruhren erkennen, ob zwischen zwei Ereignissen eine kausale Abhängigkeit besteht oder nicht.

Take away

Wenn es um das Konzept der Zeit im verteilten System geht, besteht das Hauptziel darin, die richtige Reihenfolge der Ereignisse zu erreichen. Ereignisse können entweder in chronologischer Reihenfolge mit physischen Uhren oder in logischer Reihenfolge mit Lamtports logischen Uhren und Vektoruhren entlang der Ausführungszeitleiste positioniert werden.

Was kommt als nächstes?

Als nächstes in der Serie werden wir darauf eingehen, wie die Zeitsynchronisation überraschend einfache Antworten auf einige klassische Probleme in verteilten Systemen geben kann: höchstens eine Nachricht , Cache-Konsistenz und gegenseitiger Ausschluss .

Leslie Lamport: Zeit, Uhren und die Reihenfolge von Ereignissen in einem verteilten System. 1978.

Barbara Liskov: Praktische Anwendungen synchronisierter Uhren in verteilten Systemen. 1993.

Maarten van Steen, Andrew S. Tanenbaum: Verteilte Systeme. 2017.

Barbara Liskov, Liuba Shrira, John Wroclawski: Effiziente At-Most-Once-Nachrichten basierend auf synchronisierten Uhren. 1991.

Cary G. Gray, David R. Cheriton: Leases: Ein effizienter fehlertoleranter Mechanismus für die Konsistenz des verteilten Dateicaches. 1989.

Ricardo Gusella, Stefano Zatti: Die Genauigkeit der Taktsynchronisation erreicht durch TEMPO in Berkeley UNIX 4.3BSD. 1989.