5.8 Wussten Sie, dass die meisten Niederschläge aus Kollisionskoaleszenz stammen?
5.8 Wussten Sie, dass die meisten Niederschläge von Kollisionskoaleszenz herrühren?
Es gibt zwei Arten von Prozessen für das Wachstum in Niederschlagstropfen: warme Wolkenprozesse und kalte Wolkenprozesse. In warmen Wolken sind alle Prozesse nur mit Flüssigkeitstropfen verbunden. In kalten Wolken können die Prozesse nur feste Partikel sowie gemischte Phasen (sowohl unterkühlte Flüssigkeit als auch Eis) umfassen. Zu den wichtigsten Prozessen gehören Kollisionen zwischen flüssigen oder festen Tropfen.
Kollisionen
Kollisionen treten sowohl in kalten als auch in warmen Wolken auf und können entweder Flüssigkeitstropfen oder feste Partikel oder beides beinhalten.
- Kollision-Koaleszenz: Großer Flüssigkeitstropfen fängt kleinere Flüssigkeitstropfen ab, wenn er fällt.
- Riming: Fallendes Eis sammelt flüssiges Wasser, das auf seiner Oberfläche gefriert.
- Einfangen der Keimbildung: Ein großer Flüssigkeitstropfen fängt kleine Eispartikel ein, die als Eiskern wirken und das Einfrieren des großen Tropfens bewirken. Das Partikel, das gesammelt wird, kann entweder ein Eiskern (IN) oder ein Stück Eis sein, das auch ein guter Eiskern ist. In beiden Fällen gefriert der unterkühlte Flüssigkeitstropfen bei Kontakt mit dem IN.
- Aggregation: Fallende Schneeflocken fangen andere Schneeflocken, die sich zu einem größeren Schneeflockenbündel zusammenschließen.
Für einen Wolkentropfen in Ruhe ist die Schwerkraft die einzige äußere Kraft. Sobald der Wolkentropfen zu fallen beginnt, bildet der Luftwiderstand eine andere Kraft, die als Widerstand bezeichnet wird und eine Funktion der Geschwindigkeit ist.
In weniger als einer Sekunde erreicht das Teilchen eine solche Fallgeschwindigkeit, dass die Widerstandskraft die Gravitationskraft genau ausgleicht und die Geschwindigkeit konstant wird. Diese Geschwindigkeit wird als Endgeschwindigkeit bezeichnet. Da die Gravitationskraft vom Volumen des Tropfens abhängt, gilt sie als Würfel des Tropfenradius. Im Gegensatz dazu wirkt der Widerstand auf die Oberfläche des Tropfens und hängt daher vom Tropfenbereich ab und gilt als Quadrat des Tropfenradius (mal der Geschwindigkeit). Wenn man die Gravitations- und Schleppkräfte gleich anderen einstellt und dann die Endgeschwindigkeit löst, kann man leicht zeigen, dass die Endgeschwindigkeit linear mit dem Fallradius variieren sollte. Messungen bestätigen diese lineare Beziehung. Zum Beispiel beträgt die Endgeschwindigkeit eines Abfalls mit einem Radius von 50 µm etwa 0,3 m s–1, während die Endgeschwindigkeit für einen 10–mal größeren Tropfen (500 µm Radius) etwa 4 m s-1 beträgt, was nur ein wenig mehr ist als ein Faktor-von-10 erhöhen.
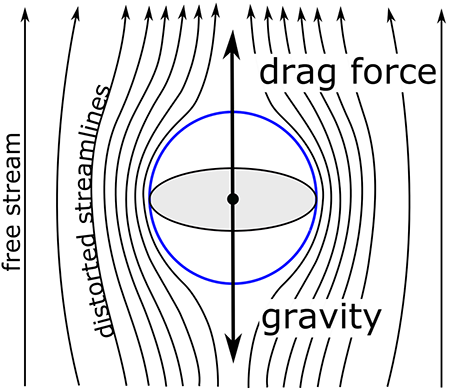
Das Wachstum eines Wolkentropfens zu einem Niederschlagstropfen durch Kollisionskoaleszenz ist gegeben durch die Gleichung:
d m L dt =ausgefegte Fläche⋅Effizienz der Sammlung⋅ Geschwindigkeitsdifferenz ⋅flüssiger Wassergehalt d m L dt = A g ⋅ E c ⋅(v L − v s) ⋅LWC d m L dt =π (r L + r s) 2 ⋅ E c ⋅ (v L − v s)⋅LWC Diese Gleichung wird aufgrund eines inkompatiblen Browsers nicht richtig dargestellt. Eine Liste der kompatiblen Browser finden Sie unter Technische Anforderungen in der Orientierung.
- mL ist die Masse des fallenden großen Tropfens,
- Ag ist die geometrische Querschnittsfläche, für die Kollisionen zwischen dem fallenden großen Tropfen und den vielen Tropfen darunter möglich sind,
- Ec ist die Kollisions-Koaleszenz-Effizienz (d.h. der Bruchteil der tatsächlichen Querschnittsfläche ist, die im Vergleich zu der geometrisch möglichen Querschnittsfläche herausgefegt wird (kleinere Tropfen können Luftströmungen folgen und den großen Tropfen umgehen) (siehe Abbildung unten),
- vL ist die Geschwindigkeit des großen Tropfens und vs ist die Geschwindigkeit der kleineren, langsamer fallenden Tropfen darunter,
- und LWC ist der flüssige Wassergehalt.
Die folgende Abbildung liefert ein gutes konzeptionelles Bild der Kollisionskoaleszenz. Der Kollektortropfen muss schneller fallen als der kleinere gesammelte Tropfen, damit die beiden kollidieren können. Wenn sich die Luftströmungen um den Tropfen ausbeugen, tragen sie die kleineren Tropfen mit sich um den Tropfen herum, und die effektive Querschnittsfläche wird kleiner als die tatsächliche Querschnittsfläche, die einfach die Querschnittsfläche einer Scheibe mit einem Radius ist, der die Summe der Radien des großen Sammeltropfens und der kleineren gesammelten Tropfen ist. Wenn Tropfen größer werden, haben sie zu viel Trägheit, um den Luftströmungen zu folgen, was die Kollision wahrscheinlicher macht.
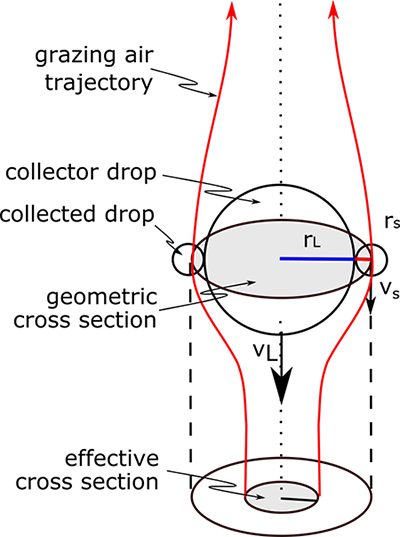
Ec ist für 10 µm Tropfen klein, so dass durch einen zufälligen Prozess einige Tropfen größer werden als andere und beginnen, kleinere Tropfen zu sammeln (siehe Abbildung unten). Ec nimmt zu, wenn der Radius des fallenden Tropfens zunimmt. Wenn der größere fallende Tropfen einen Radius von mehr als 100 µm erreicht, ist seine Kollisionskoaleszenzeffizienz für alle kleineren Tropfen bis zu Größen von etwa 10-20 µm sehr gut.
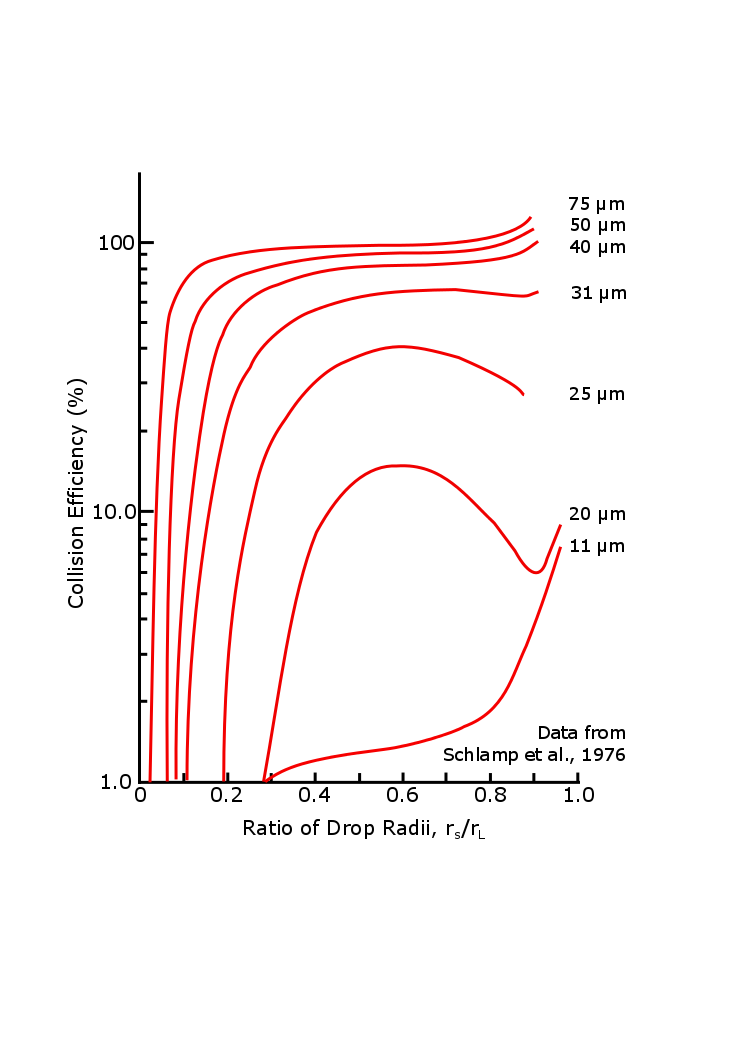
Sobald ein Sammeltropfen einen Radius von einigen hundert µm erreicht hat, fällt er schnell (vL > > vs) und seine Kollisionskoaleszenzeffizienz liegt nahe bei 100%. Führen Sie nun die folgenden Schritte aus, um Gleichung 5.16 neu zu schreiben: (1) Ec gleich 1, (2) vL >> vs, (3) vL = Konstante x rL, (4) mL = 4plnrL3 / 3 und (5) löse nach drL / dt. Sobald Sie diese Schritte ausführen, können Sie zeigen, dass drL / dt proportional zu rL ist. Das heißt, je größer der Tropfen wird, desto schneller wächst er. Die Trennung von Variablen (rL und t) und die Integration von rL = 0 bei t = 0 in beliebige Werte von rL und t zeigt, dass rL exponentiell mit der Zeit zunimmt:
r d ∝exp(Zeit) Diese Gleichung wird aufgrund eines inkompatiblen Browsers nicht richtig gerendert. Eine Liste der kompatiblen Browser finden Sie unter Technische Anforderungen in der Orientierung.
Mit der Proportionalitätskonstante zwischen Endgeschwindigkeit und Fallradius auf 0 gesetzt.8 x 10-3 s–1 und LWC = 1 g m–3 kann gezeigt werden, dass ein Tropfen durch Kollisionskoaleszenz in nur 25 Minuten von 50 µm auf 1000 µm wachsen kann. So wachsen die aktivierten Wolkentropfen durch das langsame Wachstum der Gasphasenabscheidung (Quadratwurzel der Zeit) auf 10-20 µm. Wenn dann die Kollisionskoaleszenz beginnt und einige große Tropfen erzeugt, können sie mit der Zeit exponentiell wachsen.
Kleinere Tropfen sind typischerweise kugelförmig. Sobald diese Tropfen einen Radius von über einem mm haben, Sie werden zunehmend verzerrt, mit einem abgeflachten Boden aufgrund von Widerstandskräften, und sie sehen ein wenig aus wie die obere Hälfte eines Hamburgerbrötchen. Sie können weiter verzerrt werden, so dass die Mitte der Brötchenform durch die Schleppkräfte nach oben gedrückt wird, so dass der Tropfen eine Form annimmt, die einer umgedrehten Schüssel ähnelt.
Schließlich brechen die Tropfen auf, entweder indem sie in der Mitte dünn genug werden, dass sie in Stücke brechen, oder indem sie mit anderen Tropfen so hart kollidieren, dass Filamente oder Flüssigkeitsblätter abbrechen, um andere Tropfen zu bilden. Diese Prozesse erzeugen eine ganze Reihe von Tropfengrößen. So besteht Regen aus Tropfen, die ein breites Spektrum an Größen haben. Das folgende Video (2:50) mit dem Titel “How Raindrops are Formed” beginnt mit einer vereinfachten Ansicht des Wasserkreislaufs der Atmosphäre, zeigt dann jedoch Beispiele für einen fallenden Tropfen, Kollisionskoaleszenz und das Aufbrechen von Wolkentropfen.
Dies ist eine vertraute Szene. Die Sonnenwärme bewirkt, dass Wasser aus Pflanzen, Seen und Ozeanen von einer Flüssigkeit in einen Dampf umgewandelt wird. Hoch in der Atmosphäre kühlt der Wasserdampf dann ab und kondensiert von einem Gas zurück zu einer Flüssigkeit. Das flüssige Wasser fällt dann in Form von Regen, Schnee, Eis oder Hagel an die Oberfläche zurück. Wasser fließt in Bäche, Seen und Ozeane ab oder wird im Boden oder in Schneewegen gespeichert. Dies ist der Wasserkreislauf und beschreibt unsere wichtigste Ressource, die sich durch das gesamte Erdsystem bewegt, aber wie die meisten Dinge auf unserer Welt können wir, wenn wir uns die winzigen Teile ansehen, aus denen das Ganze besteht, viel mehr über das Phänomen erfahren. Nehmen Sie die Form eines einzelnen Regentropfens an. Kleine Wassertröpfchen in der Atmosphäre sind aufgrund der Oberflächenspannung oder Haut der Wassermoleküle kugelförmig. Wenn diese Tröpfchen wachsen, werden sie schwerer und beginnen durch die Luft zu fallen. Wenn sie fallen, kollidiert der Regentropfen mit anderen Tropfen und wird immer größer. Diese größeren Regentropfen fallen schneller durch die Luft Der Windwiderstand an der Unterseite des Tropfens bewirkt, dass sich der Boden des Tropfens abflacht, was zu einem Tropfen führt, der wie ein Hamburgerbrötchen aussieht. Wenn der Tropfen weiter fällt und irgendwann wächst, wird er zu groß, als dass die Oberflächenspannung ihn zusammenhalten könnte, sodass der Regentropfen in kleinere Spiracle-Tropfen zerbricht. Die Prozesse zu untersuchen, die wir mit bloßem Auge nicht sehen können, ist nichts Neues. Wissenschaft und Technik treiben sich gegenseitig voran und führen oft zu Erkenntnissen und Entdeckungen. Mit der Erfindung der Hochgeschwindigkeitsfotografie sahen wir endlich die grundlegendsten Elemente unseres wässrigen Planeten in Aktion. Zu verstehen, wie ein winziger Regentropfen durch die Atmosphäre fällt, entlarvt nicht nur den Mythos, dass ein Regentropfen wie eine Träne fällt. Es macht tatsächlich einen Unterschied, wenn es darum geht, Niederschlag insbesondere für Bodenradargeräte zu messen. Bodenradare betrachten die Seiten der Regentropfen und schätzen dann die vertikalen und horizontalen Seufzer. Ein schwererer, flacherer Tropfen ermöglicht es Radaren, schwerere Niederschläge zu identifizieren. Tatsächlich können die beiden Radargeräte an Bord des GPM-Satelliten auch Tropfengrößen aus dem Weltraum messen, und ein genauerer Blick auf Regentropfen gibt uns einen genaueren Blick darauf, wie sich der globale Niederschlag entwickelt.
Für Riming, Einfangkeimbildung und Aggregation gibt es ähnliche Gleichungen mit ähnlichen Begriffen wie in Gleichung 5.16 — eine ausgefegte Fläche, eine Sammeleffizienz, die Relativgeschwindigkeit und die flüssige oder feste Massenkonzentration der kleineren Tropfen oder des Eises. Diese sind in der Regel etwas komplizierter, wenn das Eis nicht kugelförmig ist, aber die Konzepte sind die gleichen. Diese Eiskollisions-Koaleszenzprozesse können Eispartikel erzeugen, die groß genug sind, um zu fallen, und wenn sich diese Partikel erwärmen, wenn sie den warmen Teil der Wolke passieren, können sie sich in flüssigen Regen verwandeln. Ein erheblicher Teil des Regens im Sommer kann von Eiskollisionskoaleszenzprozessen oberhalb der Gefrierlinie in den Wolken stammen.