Computational grafer

Backpropagation implementeres i dybe læringsrammer som Tensorstrøm, fakkel, Theano osv., ved hjælp af beregningsgrafer. Mere markant kombinerer forståelse af bagudbredelse på beregningsgrafer flere forskellige algoritmer og dens variationer, såsom backprop gennem tid og backprop med delte vægte. Når alt er konverteret til en beregningsgraf, er de stadig den samme algoritme − bare tilbage udbredelse på beregningsgrafer.

Hvad er Beregningsgraf

en beregningsgraf er defineret som en rettet graf, hvor knudepunkterne svarer til matematiske operationer. Beregningsgrafer er en måde at udtrykke og evaluere et matematisk udtryk på.

for eksempel er her en simpel matematisk ligning −

$$p = +y$$

vi kan tegne en beregningsgraf af ovenstående ligning som følger.

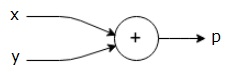
ovenstående beregningsgraf har en tilføjelsesknude (node med “+” tegn) med to inputvariabler og y og en output k.

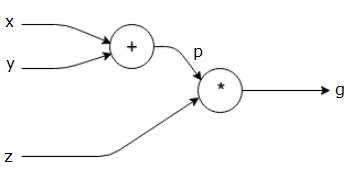
lad os tage et andet eksempel, lidt mere komplekst. Vi har følgende ligning.

$$g = \venstre (h+y \højre ) \ast $$

ovenstående ligning er repræsenteret af følgende beregningsgraf.

Computational grafer og Backpropagation

Computational grafer og backpropagation, begge er vigtige kernebegreber i dyb læring til træning af neurale netværk.

Fremadpas

Fremadpas er proceduren for evaluering af værdien af det matematiske udtryk repræsenteret af beregningsgrafer. Gør fremad pass betyder, at vi passerer værdien fra variabler i fremadgående retning fra venstre (input) til højre, hvor output er.

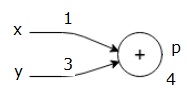
lad os overveje et eksempel ved at give en vis værdi til alle input. Antag, at følgende værdier gives til alle input.

$ $ = 1, y=3, å=-3$$

ved at give disse værdier til indgangene kan vi udføre fremadgående pass og få følgende værdier for udgangene på hver node.

først bruger vi værdien af H = 1 og y = 3 for at få p = 4.

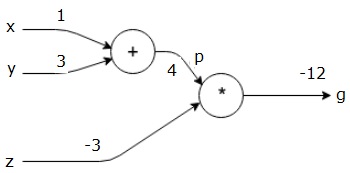
så bruger vi p = 4 og å = -3 for at få g = -12. Vi går fra venstre mod højre, fremad.

mål for baglæns Pass

i baglæns pass er vores hensigt at beregne gradienterne for hver indgang i forhold til den endelige output. Disse gradienter er vigtige for træning af det neurale netværk ved hjælp af gradientafstamning.

for eksempel ønsker vi følgende gradienter.

ønskede gradienter

$$\frac{\partial f} {\partial f},\frac{\partial y} {\partial f},\frac{\partial f} {\partial f} {\partial f}

baglæns pass (backpropagation)

vi starter baglæns pass ved at finde derivatet af den endelige output med hensyn til den endelige output (selv!). Således vil det resultere i identitetsafledning, og værdien er lig med en.

$$\frac{\partial g}{\partial g} = 1$$

vores beregningsgraf ser nu ud som vist nedenfor –

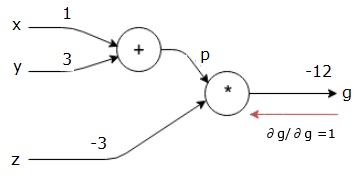
næste, vi vil gøre baglæns gennem “*” operationen. Vi beregner gradienterne ved p og å. Da g = p * å, ved vi det−

$$\frac {\partial g} {\partial å} = p$$

$$\frac {\partial g} {\partial p} = å $ $

vi kender allerede værdierne for å og p fra det forreste pas. Derfor får vi−

$$\frac {\partial g} {\partial å} = p = 4$$

og

$$\frac {\partial g} {\partial p} = å = -3$$

vi ønsker at beregne gradienterne ved H og y−

$$\frac {\partial g}, \frac {\partial g} {\partial y}$$

vi ønsker dog at gøre dette effektivt (selvom h og g kun er to humle væk i denne graf, kan du forestille dig, at de er virkelig langt fra hinanden). For at beregne disse værdier effektivt bruger vi kædereglen for differentiering. Fra Kæde Regel, vi har−

$$\frac {\partial g} {\partial g}=\frac {\partial g} {\partial p} \ ast \frac {\partial p} {\partial s}}$$

$$\ frac {\partial g} {\partial y}=\frac {\partial g} {\partial p} \ ast \frac {\partial p} {\partial y} $ $

men vi ved allerede, at dg/dp = -3, dp/DKS og dp/Dy er lette, da p direkte afhænger af H og y. Vi har –

$ $ p=S + y \ højre pil \frac {\delvis s} {\delvis s} = 1, \frac {\delvis y} {\delvis s} = 1$$

derfor får vi−

$$\frac {\partial g} {\partial f} = \frac {\partial g} {\partial p} \ ast \frac {\partial p} {\partial f} = \ left (-3 \right ).1 = -3$$

derudover for input y−

$$\frac {\partial g} {\partial y} = \frac {\partial g} {\partial p} \ ast \frac {\partial p} {\partial y} = \ left (-3 \right ).1 = -3$$

hovedårsagen til at gøre dette baglæns er, at når vi skulle beregne gradienten ved h, brugte vi kun allerede beregnede værdier og DKV/DKV (derivat af node output i forhold til den samme node input). Vi brugte lokal information til at beregne en global værdi.

trin til træning af et neuralt netværk

Følg disse trin for at træne et neuralt netværk−

• for datapunkter i datasæt går vi fremad med input og beregner omkostningerne c som output.

• vi går baglæns fra c og beregner gradienter for alle noder i grafen. Dette inkluderer noder, der repræsenterer de neurale netværksvægte.

• vi opdaterer derefter vægtene ved at gøre V = V – læringshastighed * gradienter.

• vi gentager denne proces, indtil stopkriterierne er opfyldt.