Beräkningsgrafer

Backpropagation implementeras i djupa inlärningsramar som Tensorflow, Torch, Theano, etc., genom att använda beräkningsgrafer. Mer signifikant kombinerar förståelse för ryggutbredning på beräkningsgrafer flera olika algoritmer och dess variationer som backprop genom tiden och backprop med delade vikter. När allt har omvandlats till en beräkningsgraf är de fortfarande samma algoritm − bara tillbaka förökning på beräkningsgrafer.

Vad är Beräkningsgraf

en beräkningsgraf definieras som en riktad graf där noderna motsvarar matematiska operationer. Beräkningsgrafer är ett sätt att uttrycka och utvärdera ett matematiskt uttryck.

här är till exempel en enkel matematisk ekvation −

$$p = x+y$$

vi kan rita ett beräkningsdiagram över ovanstående ekvation enligt följande.

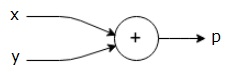
ovanstående beräkningsgraf har en tilläggsnod (nod med ” + ” – tecken) med två ingångsvariabler x och y och en Utgång q.

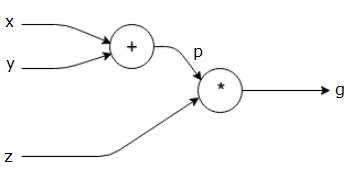
Låt oss ta ett annat exempel, något mer komplext. Vi har följande ekvation.

$$g = \vänster (x+Y \höger ) \ast z $$

ovanstående ekvation representeras av följande beräkningsdiagram.

Computational grafer och Backpropagation

Computational grafer och backpropagation, båda är viktiga kärnkoncept i djupt lärande för utbildning neurala nätverk.

Framåtpass

Framåtpass är proceduren för att utvärdera värdet av det matematiska uttrycket som representeras av beräkningsgrafer. Att göra framåtpass betyder att vi passerar värdet från variabler i framåtriktning från vänster (ingång) till höger där utgången är.

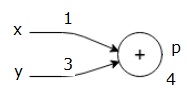
låt oss överväga ett exempel genom att ge något värde till alla ingångar. Antag att följande värden ges till alla ingångar.

$ $ x=1, y = 3, z=-3$$

genom att ge dessa värden till ingångarna kan vi utföra framåtpass och få följande värden för utgångarna på varje nod.

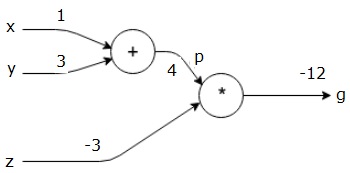
först använder vi värdet x = 1 och y = 3 för att få p = 4.

då använder vi p = 4 och z = -3 för att få g = -12. Vi går från vänster till höger, framåt.

mål för Bakåtpass

i bakåtpasset är vår avsikt att beräkna lutningarna för varje ingång med avseende på den slutliga utgången. Dessa gradienter är viktiga för att träna det neurala nätverket med hjälp av gradient nedstigning.

till exempel önskar vi följande gradienter.

önskade gradienter

$$ \ frac {\partial x} {\partial f}, \ frac {\partial y} {\partial f}, \frac {\partial z} {\partial f}$ $

Bakåtpass (backpropagation)

vi startar bakåtpasset genom att hitta derivatet av den slutliga utgången med avseende på den slutliga utgången (själv!). Således kommer det att resultera i identitetsavledningen och värdet är lika med ett.

$ $ \ frac {\partiell g} {\partiell g} = 1$$

vår beräkningsgraf ser nu ut som visas nedan –

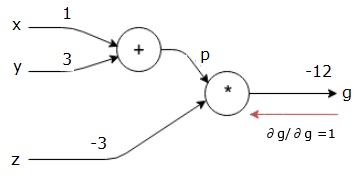
därefter kommer vi att göra bakåtpasset genom ” * ” – operationen. Vi kommer att beräkna gradienterna vid p och z. eftersom g = p * z vet vi det−

$$\frac {\partial g} {\partial z} = p$$

$$\frac {\partial g} {\partial p} = z$ $

vi vet redan värdena för z och p från framåtpasset. Därför får vi−

$$\frac {\partial g} {\partial z} = p = 4$$

och

$$ \ frac {\partiell g} {\partiell p} = z = -3$$

vi vill beräkna gradienterna vid x och y−

$$\frac{\partial g}{\partial x}, \frac{\partial g}{\partial y}$$

men vi vill göra detta effektivt (även om x och g bara är två humle bort i den här grafen, föreställ dig att de är riktigt långt ifrån varandra). För att beräkna dessa värden effektivt kommer vi att använda kedjeregeln för differentiering. Från chain rule har vi−

$$\frac {\partial g} {\partial x}= \ frac {\partial g} {\partial p} \ ast \ frac {\partial p} {\partial x}$$

$$\frac{\partial g}{\partial y}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial y}$$

men vi vet redan att dg/dp = -3, dp/dx och dp/dy är enkla eftersom p direkt beror på x och y. Vi har –

$$p = x + y\Rightarrow \ frac {\partiell x} {\partiell p} = 1, \frac {\partiell y} {\partiell p} = 1$$

därför får vi−

$$\frac {\partiell g} {\partiell f} = \ frac {\partiell g} {\partiell p} \ ast \ frac {\partiell p} {\partiell x} = \ vänster (-3 \ höger).1 = -3$$

dessutom, för ingången y−

$$\frac {\partiell g} {\partiell y} = \ frac {\partiell g} {\partiell p} \ ast \ frac {\partiell p} {\partiell y} = \ vänster (-3 \ höger).1 = -3$$

huvudskälet till att göra detta bakåt är att när vi var tvungna att beräkna gradienten vid x använde vi bara redan beräknade värden och dq/dx (derivat av nodutgång med avseende på samma nods ingång). Vi använde lokal information för att beräkna ett globalt värde.

steg för att träna ett neuralt nätverk

följ dessa steg för att träna ett neuralt nätverk−

• för datapunkt x i dataset passerar vi framåt med x som ingång och beräknar kostnaden c som utgång.

• vi gör bakåt passerar börjar vid c, och beräkna gradienter för alla noder i grafen. Detta inkluderar noder som representerar neurala nätverksvikter.

• vi uppdaterar sedan vikterna genom att göra w = w – learning rate * gradienter.

• vi upprepar denna process tills stoppkriterierna är uppfyllda.