Grafici computazionali

Backpropagation è implementato in framework di apprendimento profondo come Tensorflow,Torch, Theano, ecc., usando grafici computazionali. Più significativamente, la comprensione della propagazione posteriore sui grafici computazionali combina diversi algoritmi e le sue variazioni come backprop nel tempo e backprop con pesi condivisi. Una volta che tutto viene convertito in un grafico computazionale, sono ancora lo stesso algoritmo − solo indietro propagazione su grafici computazionali.

Cos’è il grafico computazionale

Un grafico computazionale è definito come un grafico diretto in cui i nodi corrispondono a operazioni matematiche. I grafici computazionali sono un modo di esprimere e valutare un’espressione matematica.

Ad esempio, ecco una semplice equazione matematica −

p p = x+y

Possiamo disegnare un grafico computazionale dell’equazione sopra come segue.

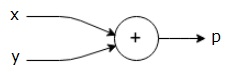
Il grafico computazionale di cui sopra ha un nodo di addizione (nodo con segno”+”) con due variabili di input x e y e un’uscita q.

Prendiamo un altro esempio, leggermente più complesso. Abbiamo la seguente equazione.

g g = \left (x+y \right ) \ast z z

L’equazione di cui sopra è rappresentata dal seguente grafico computazionale.

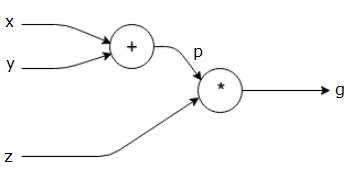
Computational Graphs and Backpropagation

Computational graphs and backpropagation, entrambi sono importanti concetti fondamentali nel deep learning per la formazione delle reti neurali.

Forward Pass

Forward pass è la procedura per valutare il valore dell’espressione matematica rappresentata dai grafici computazionali. Fare forward pass significa che stiamo passando il valore dalle variabili in avanti da sinistra (input) a destra dove si trova l’output.

Consideriamo un esempio dando un certo valore a tutti gli input. Supponiamo che i seguenti valori siano dati a tutti gli input.

x x = 1, y=3, z=-3$$

Dando questi valori agli input, possiamo eseguire forward pass e ottenere i seguenti valori per le uscite su ciascun nodo.

In primo luogo, usiamo il valore di x = 1 e y = 3, per ottenere p = 4.

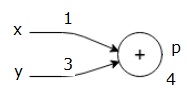
Quindi usiamo p = 4 e z = -3 per ottenere g = -12. Andiamo da sinistra a destra, avanti.

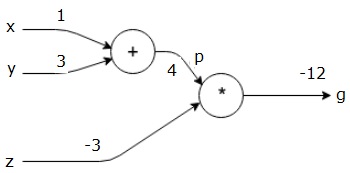
Objectives of Backward Pass

Nel backward pass, la nostra intenzione è quella di calcolare i gradienti per ogni ingresso rispetto all’uscita finale. Questi gradienti sono essenziali per allenare la rete neurale usando la discesa del gradiente.

Ad esempio, desideriamo i seguenti gradienti.

Gradienti desiderati

\\frac {\partial x} {\partial f},\frac {\partial y} {\partial f},\frac {\partial z} {\partial f}

Passaggio all’indietro (backpropagation)

Iniziamo il passaggio all’indietro trovando la derivata dell’output finale rispetto all’output finale (stesso!). Quindi, si tradurrà nella derivazione dell’identità e il valore è uguale a uno.

$ $ \frac{\partial g}{\partial g} = 1$$

Il nostro grafico computazionale ora appare come mostrato di seguito –

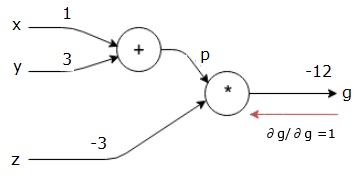
Successivamente, faremo il backward pass attraverso l’operazione”*”. Calcoleremo i gradienti a p e z. Poiché g = p * z, sappiamo che−

$$\frac {\partial g} {\partial z} = p$$

$$\frac {\partial g} {\partial p} = z

Conosciamo già i valori di z e p dal passaggio in avanti. Quindi, si ottiene−

$$\frac{\partial g}{\partial z} = p = 4$$

e

$$\frac{\partial g}{\partial p} = z = -3$$

vogliamo calcolare le pendenze in x e y−

$$\frac{\partial g}{\partial x}, \frac{\partial g}{\partial y}$$

Tuttavia, si vuole fare questo in modo efficiente (anche se x e g sono solo due passaggi in questo grafico, immaginare di essere davvero lontani l’uno dall’altro). Per calcolare questi valori in modo efficiente, useremo la regola della catena di differenziazione. Dalla catena di regola, abbiamo−

$$\frac{\partial g}{\partial x}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial x}$$

$$\frac{\partial g}{\partial y}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial y}$$

Ma sappiamo già il dg/dp = -3, dp/dx e dp/dy sono facili poiché p dipende direttamente da x e y. Abbiamo −

$$p=x+y\Rightarrow \frac{\partial x}{\partial p} = 1, \frac{\partial y}{\partial p} = 1$$

Quindi, si ottiene−

$$\frac{\partial g} {\partial f} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial x} = \left ( -3 \a destra ).1 = -3$$

Inoltre, per l’ingresso y−

$$\frac {\partial g} {\partial y} = \ frac {\partial g} {\partial p} \ ast \ frac {\partial p} {\partial y} = \ left (-3 \right ).1 = -3$$

Il motivo principale per farlo all’indietro è che quando abbiamo dovuto calcolare il gradiente a x, abbiamo usato solo valori già calcolati e dq / dx (derivata dell’output del nodo rispetto all’input dello stesso nodo). Abbiamo usato le informazioni locali per calcolare un valore globale.

Passi per addestrare una rete neurale

Seguire questi passaggi per addestrare una rete neurale−

• Per il punto di dati x nel set di dati, passiamo in avanti con x come input e calcoliamo il costo c come output.

• Facciamo il passaggio all’indietro a partire da c e calcoliamo i gradienti per tutti i nodi nel grafico. Ciò include i nodi che rappresentano i pesi della rete neurale.

• Quindi aggiorniamo i pesi facendo W = W-learning rate * gradienti.

• Ripetiamo questo processo fino a quando i criteri di stop non sono soddisfatti.