grafice computaționale

Backpropagation este implementat în cadre de învățare profundă, cum ar fi Tensorflow, Torch, Theano, etc., prin utilizarea graficelor de calcul. Mai semnificativ, înțelegerea propagării înapoi pe graficele de calcul combină mai mulți algoritmi diferiți și variațiile sale, cum ar fi backprop în timp și backprop cu greutăți partajate. Odată ce totul este transformat într − un grafic de calcul, acestea sunt în continuare același algoritm-doar propagarea înapoi pe graficele de calcul.

ce este graficul de calcul

un grafic de calcul este definit ca un grafic direcționat în care nodurile corespund operațiilor matematice. Graficele computaționale sunt o modalitate de exprimare și evaluare a unei expresii matematice.

de exemplu, aici este o ecuație matematică simplă −

$$p = x+y$$

putem desena un grafic de calcul al ecuației de mai sus, după cum urmează.

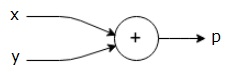
graficul de calcul de mai sus are un nod de adăugare (nod cu semnul”+”) cu două variabile de intrare x și y și o ieșire q.

să luăm un alt exemplu, puțin mai complex. Avem următoarea ecuație.

$$g = \stânga (X+Y \dreapta ) \ast z $$

ecuația de mai sus este reprezentată de următorul grafic de calcul.

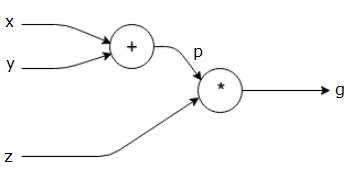
graficele computaționale și Backpropagarea

graficele computaționale și backpropagarea, ambele sunt concepte de bază importante în învățarea profundă pentru formarea rețelelor neuronale.

Forward Pass

forward pass este procedura de evaluare a valorii expresiei matematice reprezentate de graficele computaționale. Făcând trecere înainte înseamnă că trecem valoarea variabilelor în direcția înainte de la stânga (intrare) la dreapta unde este ieșirea.

să luăm în considerare un exemplu dând o anumită valoare tuturor intrărilor. Să presupunem că următoarele valori sunt date tuturor intrărilor.

$ $ x = 1, y = 3, z=-3$$

dând aceste valori intrărilor, putem efectua trecerea înainte și obținem următoarele valori pentru ieșirile de pe fiecare nod.

în primul rând, vom folosi valoarea x = 1 și y = 3, pentru a obține p = 4.

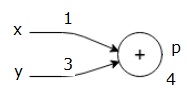
apoi vom folosi p = 4 și z = -3 pentru a obține g = -12. Mergem de la stânga la dreapta, înainte.

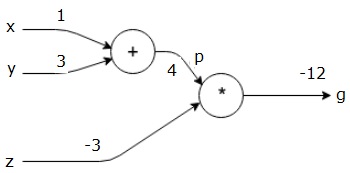
obiectivele pas înapoi

în pasul înapoi, intenția noastră este de a calcula gradienții pentru fiecare intrare în raport cu ieșirea finală. Acești gradienți sunt esențiali pentru antrenarea rețelei neuronale folosind coborârea gradientului.

de exemplu, dorim următorii gradienți.

gradiente dorite

$$ \ frac {\partial x} {\partial F}, \frac {\partial y} {\partial F}, \frac {\partial z} {\partial F}$$

pas înapoi (backpropagation)

începem pasul înapoi găsind derivata ieșirii finale în raport cu ieșirea finală (în sine!). Astfel, va rezulta derivarea identității și valoarea este egală cu una.

$$ \ frac {\parțial g} {\parțial G} = 1$$

graficul nostru de calcul arată acum așa cum se arată mai jos −

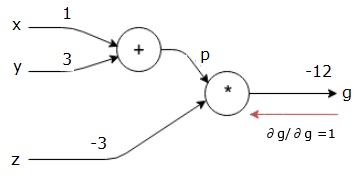
în continuare, vom face trecerea înapoi prin operația”*”. Vom calcula gradienții la p și z. deoarece g = p * z, știm că−

$$\frac {\partial g} {\partial z} = p$$

$$\frac {\partial g} {\partial p} = z $ $

știm deja valorile lui z și p Din pasul înainte. Prin urmare, obținem−

$$\frac {\partial g} {\partial z} = p = 4$$

și

$$ \ frac {\parțial g} {\parțial p} = z = -3$$

vrem să calculăm gradienții la x și y−

$$\frac {\partial g} {\partial x}, \ frac {\partial g} {\partial y} $ $

cu toate acestea, vrem să facem acest lucru eficient (deși x și g sunt doar două hamei distanță în acest grafic, imaginați-vă că sunt foarte departe unul de celălalt). Pentru a calcula aceste valori în mod eficient, vom folosi regula lanțului de diferențiere. Din regula lanțului, avem−

$$\frac {\partial g} {\partial x}= \ frac {\partial g} {\partial p} \ ast \ frac {\partial p} {\partial x}$$

$$\frac {\parțial g} {\parțial y}= \ frac {\parțial g} {\parțial p} \ ast \ frac {\parțial p} {\parțial y} $ $

dar știm deja că DG/dp = -3, dp/dx și dp/dy sunt ușoare, deoarece p depinde direct de x și y. Avem –

$ $ p = x + y\Rightarrow \ frac {\parțial x} {\parțial p} = 1, \ frac {\parțial y} {\parțial P} = 1$$

prin urmare, obținem−

$$\frac {\parțial g} {\parțial F} = \ frac {\parțial g} {\parțial p} \ast \ frac {\parțial p} {\parțial x} = \ stânga (-3 \ dreapta).1 = -3$$

în plus, pentru intrarea y−

$$\frac {\parțial g} {\parțial y} = \ frac {\parțial g} {\parțial p} \ ast \ frac {\parțial p} {\parțial y} = \ stânga (-3 \ dreapta).1 = -3$$

principalul motiv pentru a face acest lucru înapoi este că atunci când a trebuit să calculăm gradientul la x, am folosit doar valori deja calculate și dq/dx (derivat al ieșirii nodului în raport cu intrarea aceluiași nod). Am folosit informații locale pentru a calcula o valoare globală.

pași pentru formarea unei rețele neuronale

urmați acești pași pentru a instrui o rețea neuronală−

• pentru punctul de date x în setul de date, facem trecerea înainte cu x ca intrare și calculăm costul c ca ieșire.

• facem trecerea înapoi începând de la c și calculăm gradienții pentru toate nodurile din grafic. Aceasta include noduri care reprezintă greutățile rețelei neuronale.

• apoi actualizăm greutățile făcând gradienți w = w-learning rate*.

• repetăm acest proces până când sunt îndeplinite criteriile de oprire.