Computational Graphs

Backpropagation wird in Deep-Learning-Frameworks wie Tensorflow, Torch, Theano usw. implementiert. durch die Verwendung von Computational Graphs. Noch wichtiger ist, dass das Verständnis der Rückausbreitung in Berechnungsgraphen mehrere verschiedene Algorithmen und deren Variationen wie Backprop through time und backprop with shared weights kombiniert. Sobald alles in einen Berechnungsgraphen umgewandelt ist, handelt es sich immer noch um denselben Algorithmus − nur die Rückausbreitung auf Berechnungsgraphen.

Was ist Computational Graph

Ein Computational Graph ist definiert als ein gerichteter Graph, bei dem die Knoten mathematischen Operationen entsprechen. Computergraphen sind eine Möglichkeit, einen mathematischen Ausdruck auszudrücken und auszuwerten.

Zum Beispiel ist hier eine einfache mathematische Gleichung –

$$ p = x+y$$

Wir können einen Rechengraphen der obigen Gleichung wie folgt zeichnen.

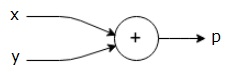
Der obige Computational Graph hat einen Additionsknoten (Knoten mit “+” -Zeichen) mit zwei Eingangsvariablen x und y und einem Ausgang q.

Nehmen wir ein anderes Beispiel, etwas komplexer. Wir haben die folgende Gleichung.

$$g = \left (x+y \right ) \ast z $$

Die obige Gleichung wird durch den folgenden Berechnungsgraphen dargestellt.

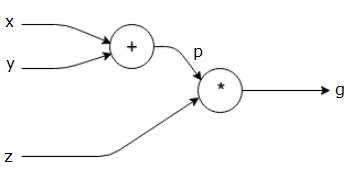
Computational Graphs und Backpropagation

Computational Graphs und Backpropagation, beide sind wichtige Kernkonzepte im Deep Learning für das Training neuronaler Netze.

Vorwärtsdurchlauf

Vorwärtsdurchlauf ist das Verfahren zur Auswertung des Wertes des mathematischen Ausdrucks, der durch Rechengraphen dargestellt wird. Vorwärtsdurchlauf bedeutet, dass wir den Wert von Variablen in Vorwärtsrichtung von links (Eingabe) nach rechts übergeben, wo sich die Ausgabe befindet.

Betrachten wir ein Beispiel, indem wir allen Eingaben einen Wert geben. Angenommen, die folgenden Werte werden für alle Eingaben angegeben.

$$x=1, y=3, z=-3$$

Indem wir diese Werte an die Eingänge übergeben, können wir einen Vorwärtsdurchlauf durchführen und die folgenden Werte für die Ausgänge auf jedem Knoten erhalten.

Zuerst verwenden wir den Wert von x = 1 und y = 3, um p = 4 zu erhalten.

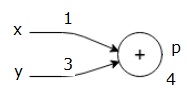
Dann verwenden wir p = 4 und z = -3, um g = -12 zu erhalten. Wir gehen von links nach rechts, vorwärts.

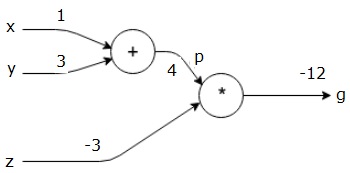
Ziele des Rückwärtsdurchlaufs

Im Rückwärtsdurchlauf ist es unsere Absicht, die Gradienten für jede Eingabe in Bezug auf die endgültige Ausgabe zu berechnen. Diese Gradienten sind für das Training des neuronalen Netzwerks mit Gradientenabstieg unerlässlich.

Zum Beispiel wünschen wir die folgenden Gradienten.

Gewünschte Gradienten

$$\frac{\partial x}{\partial f}, \frac{\partial y}{\partial f}, \frac{\partial z}{\partial f}$$

Rückwärtspass (backpropagation)

Wir beginnen den Rückwärtspass, indem wir die Ableitung der endgültigen Ausgabe in Bezug auf die endgültige Ausgabe (selbst!). Somit führt dies zur Identitätsableitung und der Wert ist gleich eins.

$$\frac{\partial g}{\partial g} = 1$$

Unser Berechnungsdiagramm sieht jetzt wie unten gezeigt aus –

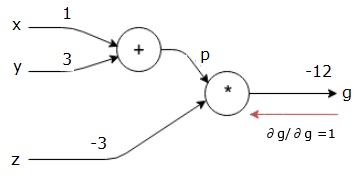
Als nächstes werden wir den Rückwärtspass durch die Operation “*” durchführen. Wir berechnen die Gradienten bei p und z. Da g = p*z , wissen wir, dass −

$$\ frac{\partielle g} {\partielle z} = p$$

$$\ frac{\partial g}{\partial p} = z$$

Wir kennen die Werte von z und p bereits aus dem Vorwärtsdurchlauf. Daher erhalten wir −

$$\ frac{\partielle g} {\partielle z} = p = 4$$

und

$$\frac{\partial g}{\partial p} = z = -3$$

Wir wollen die Gradienten an x und y berechnen −

$$\ frac {\partial g} {\partial x}, \frac{\partial g}{\partial y}$$

Wir möchten dies jedoch effizient tun (obwohl x und g in diesem Diagramm nur zwei Hops entfernt sind, stellen Sie sich vor, sie wären wirklich weit voneinander entfernt). Um diese Werte effizient zu berechnen, verwenden wir die Kettenregel der Differenzierung. Von der Kettenregel haben wir −

$$\ frac{\partial g}{\partial x}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial x}$$

$$\ frac{\partial g}{\partial y}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial y}$$

Aber wir wissen bereits, dass dg / dp = -3, dp / dx und dp / dy einfach sind, da p direkt von x und y abhängt. Wir haben –

$$p=x+y\Rightarrow \frac{\partial x}{\partial p} = 1, \frac{\partial y}{\partial p} = 1$$

Daher erhalten wir −

$$\ frac{\partial g} {\partial f} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial x} = \links ( -3 \rechts ).1 = -3$$

Zusätzlich kann für den Eingang y −

$$\ frac{\partial g} {\partial y} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial y} = \links ( -3 \rechts ).1 = -3$$

Der Hauptgrund dafür ist, dass wir bei der Berechnung des Gradienten bei x nur bereits berechnete Werte und dq / dx (Ableitung der Knotenausgabe in Bezug auf die Eingabe desselben Knotens) verwendet haben. Wir haben lokale Informationen verwendet, um einen globalen Wert zu berechnen.

Schritte zum Trainieren eines neuronalen Netzwerks

Befolgen Sie diese Schritte, um ein neuronales Netzwerk zu trainieren −

• Für den Datenpunkt x im Datensatz übergeben wir x als Eingabe und berechnen die Kosten c als Ausgabe.

• Wir führen einen Rückwärtspass ab c durch und berechnen Gradienten für alle Knoten im Diagramm. Dazu gehören Knoten, die die Gewichte des neuronalen Netzwerks darstellen.

• Wir aktualisieren dann die Gewichte, indem wir W = W – Lernrate * Gradienten ausführen.

• Wir wiederholen diesen Vorgang, bis alle Kriterien erfüllt sind.