計算グラフ

バックプロパゲーションは、Tensorflow、Torch、Theanoなどの深層学習フレームワークで実装されています。、計算グラフを使用して。 さらに重要なことに、計算グラフ上の逆伝播を理解することは、いくつかの異なるアルゴリズムと、時間によるbackpropや共有重みを持つbackpropなどのその変 すべてが計算グラフに変換されると、それらは同じアルゴリズムであり、計算グラフ上の逆伝播だけです。

計算グラフとは

計算グラフは、ノードが数学演算に対応する有向グラフとして定義されます。 計算グラフは、数式を表現し、評価する方法です。

例えば、ここでは簡単な数式です−

≤p=x+y≤

上記の方程式の計算グラフを次のように描くことができます。

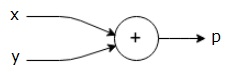
上記の計算グラフには、二つの入力変数xとyと一つの出力qを持つ加算ノード（”+”記号のノード）があります。

もう少し複雑な別の例を見てみましょう。 以下の式があります。$ $G=\左（X+Y\右）\AST z z

上記の式は、次の計算グラフで表されます。

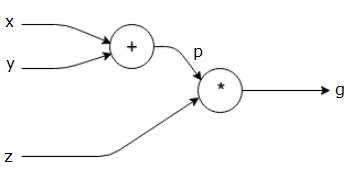
計算グラフと逆伝播

計算グラフと逆伝播は、どちらもニューラルネットワークを訓練するための深層学習における重要なコア概念である。

Forward Pass

Forward passは、計算グラフで表される数式の値を評価する手順です。 Forward passを実行すると、変数の値を左（入力）から出力がある右に順方向に渡していることを意味します。

すべての入力に何らかの値を与えることによって例を考えてみましょう。 すべての入力に次の値が与えられたとします。

≤x=1,y=3,z=-3$$

これらの値を入力に与えることによって、forward passを実行し、各ノードの出力に対して次の値を取得できます。

まず、x=1とy=3の値を使用してp=4を取得します。

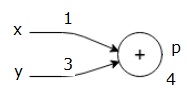
次に、p=4とz=-3を使用してg=-12を取得します。 私たちは左から右に、前方に行きます。

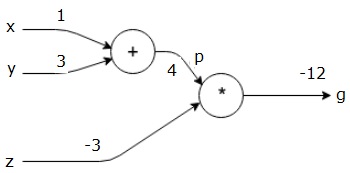
Backward Passの目的

backward passでは、最終出力に対する各入力の勾配を計算することを意図しています。 これらの勾配は，勾配降下法を用いたニューラルネットワークの訓練に不可欠である。

例えば、次のような勾配が必要です。

所望の勾配

frac\frac{\partial x}{\partial f}、\frac{\partial y}{\partial f}、\frac{\partial z}{\partial f}backward

バックワードパス（バックプロパゲーション）

最終出力に対する最終出力の導関数を見つけることによ). したがって、恒等式の導出が行われ、値は1に等しくなります。

frac\frac{\partial g}{\partial g}{のようになります。} = 1$$

計算グラフは以下のようになります−

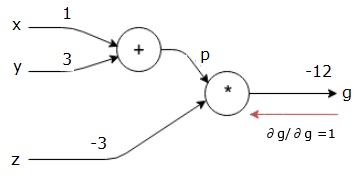
次に、”*”操作を介してbackward passを行います。 Pとzの勾配を計算します。g=p*zなので、次のことがわかります−

$$\frac frac{\partial g}{\partial z}=p fracを使用してください。$$

$$\frac frac{\partial g}{\partial p}=z$ $

フォワードパスからのzとpの値はすでにわかっています。 したがって、我々は得る−

$$\frac frac{\partial g}{\partial z}=p fracを使用してください。= 4$$

そして

frac\frac{\partial g}{\partial p}=z z= -3$$

我々はxとyで勾配を計算したい−

$$\frac frac{\partial g}{\partial x}、\frac{\partial g}{\partial y}.

しかし、これを効率的に行いたいと考えています（xとgはこのグラフでは2つのホップしか離れていませんが、実際には これらの値を効率的に計算するために、微分の連鎖規則を使用します。 鎖の規則から、私達は持っています−

$$\as frac{\partial g}{\partial x}=\frac{\partial g}{\partial p}\ast\frac{\partial p}{\partial x}=となります。}$$

$$\frac frac{\partial g}{\partial y}=\frac{\partial g}{\partial p}\ast\frac{\partial p}{\partial y}p

しかし、pはxとyに直接依存するので、dg/dp=-3、dp/dx、dp/dyはすでに知っています。 我々は持っている-

p p=x+y\rightarrow\frac{\partial x}{\partial p}=1、\frac{\partial y}{\partial p} = 1$$

したがって、我々は得る−

$$\frac frac{\partial g}{\partial f}=\frac{\partial g}{\partial p}\ast\frac{\partial p}{\partial x}=\left(-3\right)..これは、f f fがf f fの部分集合であることを示しています。1 = -3$$

また、入力yに対して−

$$\frac frac{\partial g}{\partial y}=\frac{\partial g}{\partial p}\ast\frac{\partial p}{\partial y}=\left（-3\right）。1 = -3$$

これを後方に行う主な理由は、xで勾配を計算する必要があったときに、既に計算された値とdq/dx（同じノードの入力に対するノード出力の導関数）のみを使 ローカル情報を使用してグローバル値を計算しました。

ニューラルネットワークを訓練するための手順

ニューラルネットワークを訓練するには、次の手順に従います−

• datasetのデータポイントxについては、xを入力として前方パスし、コストcを出力として計算します。

• cから逆方向にパスを開始し、グラフ内のすべてのノードの勾配を計算します。 これには、ニューラルネットワークの重みを表すノードが含まれます。

• 次に、W=W-learning rate*gradientsを実行して重みを更新します。

• 停止基準が満たされるまで、このプロセスを繰り返します。