computationele grafieken

Backpropagation wordt geïmplementeerd in deep learning frameworks zoals Tensorflow, Torch, Theano, enz., met behulp van computationele grafieken. Belangrijker nog, het begrijpen van terug voortplanting op computationele grafieken combineert verschillende algoritmen en zijn variaties zoals backprop door de tijd en backprop met gedeelde gewichten. Zodra alles is omgezet in een computationele grafiek, ze zijn nog steeds hetzelfde algoritme − gewoon terug voortplanting op computationele grafieken.

Wat is computationele grafiek

een computationele grafiek wordt gedefinieerd als een gerichte grafiek waarbij de knooppunten overeenkomen met wiskundige bewerkingen. Computationele grafieken zijn een manier om een wiskundige uitdrukking uit te drukken en te evalueren.

bijvoorbeeld, hier is een eenvoudige wiskundige vergelijking –

$$p = x+y$ $

we kunnen een computationele grafiek van de bovenstaande vergelijking als volgt tekenen.

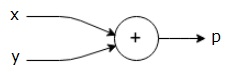
de bovenstaande computationele grafiek heeft een optellings knooppunt (knooppunt met “+” teken) met twee invoervariabelen x en y en één uitvoer q.

laten we een ander voorbeeld nemen, iets complexer. We hebben de volgende vergelijking.

$$g = \ left (x+y \right ) \ast z $$

de bovenstaande vergelijking wordt weergegeven door de volgende computationele grafiek.

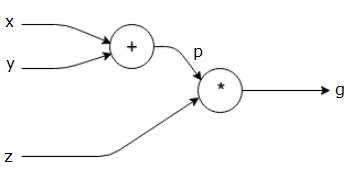
Computational Graphs and Backpropagation

Computational graphs and backpropagation, beide zijn belangrijke kernbegrippen in deep learning voor het trainen van neurale netwerken.

Forward Pass

Forward pass is de procedure voor het evalueren van de waarde van de wiskundige uitdrukking vertegenwoordigd door computationele grafieken. Forward pass doen betekent dat we de waarde van variabelen in voorwaartse richting doorgeven van links (input) naar rechts waar de output is.

laten we een voorbeeld bekijken door een waarde aan alle input te geven. Stel, de volgende waarden worden gegeven aan alle ingangen.

$$x = 1, y=3, z=-3$$

door deze waarden aan de ingangen te geven, kunnen we forward pass uitvoeren en de volgende waarden krijgen voor de uitgangen op elk knooppunt.

eerst gebruiken we de waarde x = 1 en y = 3, om p = 4 te krijgen.

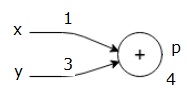
dan gebruiken we p = 4 en z = -3 om g = -12 te krijgen. We gaan van links naar rechts, vooruit.

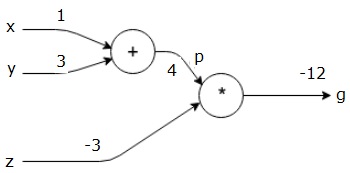
doelstellingen van achterwaartse pas

in de achterwaartse pas is het onze bedoeling om de gradiënten voor elke input te berekenen ten opzichte van de uiteindelijke output. Deze gradiënten zijn essentieel voor het trainen van het neurale netwerk met gradiëntafdaling.

bijvoorbeeld, we willen de volgende gradiënten.

gewenste gradiënten

$$ \ frac {\partial x}{\partial f}, \ frac{\partial y}{\partial f},\frac {\partial z} {\partial f}$$

achterwaartse pas (backpropagatie)

we starten de achterwaartse pas door de afgeleide van de uiteindelijke uitvoer te vinden ten opzichte van de uiteindelijke uitvoer (zelf!). Dus, het zal resulteren in de identiteit afleiding en de waarde is gelijk aan één.

$$ \ frac {\partial g} {\partial g} = 1$$

onze computationele grafiek ziet er nu uit zoals hieronder getoond –

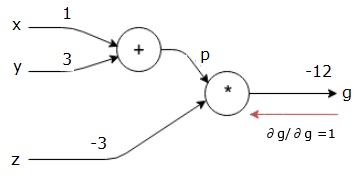
vervolgens zullen we de achterwaartse pas door de “*” operatie doen. We berekenen de gradiënten bij p en z. aangezien g = p * z, weten we dat−

$$\frac {\partial g} {\partial z} = p$$

$$\frac {\partial g} {\partial p} = z$$

we kennen de waarden van z en p al van de voorwaartse pas. Vandaar dat we−

$$\frac {\partial g} {\partial z} = p = 4$$

en

$$ \ frac {\partial g} {\partial p} = z = -3$$

we willen de verlopen berekenen op x en y−

$$\frac {\partial g}{\partial x},\frac {\partial g} {\partial y}$$

echter, we willen dit efficiënt doen (hoewel x en g slechts twee hops verwijderd zijn in deze grafiek, stel je voor dat ze heel ver van elkaar zijn). Om deze waarden efficiënt te berekenen, gebruiken we de kettingregel van differentiatie. Van de kettingregel, wij hebben−

$$\frac{\partial g}{\partial x}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial x}$$

$$\frac{\partial g}{\partial y}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial y}$$

Maar we weten al dat de dg/dp = -3, dp/dx en dp/dy eenvoudig omdat p direct afhankelijk van x en y. We hebben −

$$p=x+y \ Rightarrow \ frac {\partial x}{\partial p} = 1, \ frac{\partial y} {\partial p} = 1$$

vandaar dat we−

$$\frac {\partial g} {\partial f} = \ frac{\partial g} {\partial p} \ ast \ frac {\partial p} {\partial x} = \ left (-3 \ right).1 = -3$$

Bovendien, voor de input y−

$$\frac {\partial g} {\partial y} = \ frac{\partial g} {\partial p} \ ast \ frac {\partial p} {\partial y} = \ left (-3 \ right).1 = -3$$

de belangrijkste reden om dit achterstevoren te doen is dat wanneer we de gradiënt op x moesten berekenen, we alleen al berekende waarden gebruikten, en dq / dx (afgeleide van knooppuntuitvoer ten opzichte van de invoer van hetzelfde knooppunt). We gebruikten lokale informatie om een globale waarde te berekenen.

stappen voor het trainen van een neuraal netwerk

volg deze stappen om een neuraal netwerk te trainen−

• voor gegevenspunt x in dataset, doen we forward pass met x als input, en berekenen de kosten c als output.

• we passen achteruit vanaf c en berekenen gradiënten voor alle knooppunten in de grafiek. Dit omvat knooppunten die de neurale netwerkgewichten vertegenwoordigen.

• vervolgens werken we de gewichten bij door W = W – learning rate * gradiënten te doen.

• we herhalen dit proces totdat aan de stopcriteria is voldaan.