Výpočetní Grafy

Backpropagation je realizován v hluboké učení rámců, jako Tensorflow, Pochodeň, Theano, atd., pomocí výpočetních grafů. Více významně, pochopení šíření na výpočetní grafy kombinuje několik různých algoritmů a jeho variace jako backprop přes čas a backprop se společnou závaží. Jakmile je vše převedeno na výpočetní graf, jsou stále stejným algoritmem-jen zpět šíření na výpočetních grafech.

Co je Výpočetní Graf

výpočetní graf je definován jako orientovaný graf, kde uzly odpovídají matematické operace. Výpočetní grafy jsou způsob vyjádření a hodnocení matematického výrazu.

například, tady je jednoduchá matematická rovnice −

$$p = x+y$$

můžeme nakreslit výpočetní graf z výše uvedené rovnice následovně.

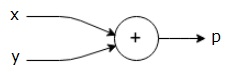
výše uvedené výpočetní graf má kromě uzlu (uzel s “+” sign) se dvěma vstupními proměnnými x a y a jeden výstup q.

vezměme si další příklad, o něco složitější. Máme následující rovnici.

$$g = \ left (x+y \right) \ast z $$

výše uvedená rovnice je reprezentována následujícím výpočetním grafem.

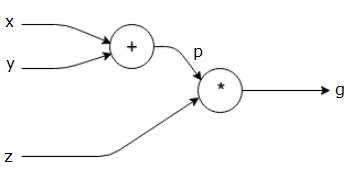
Výpočetní Grafy a Backpropagation

Výpočetní grafy a backpropagation, jak jsou důležité základní pojmy v hluboké učení pro trénink neuronové sítě.

Forward Pass

Forward pass je postup pro vyhodnocení hodnoty matematického výrazu reprezentovaného výpočetními grafy. Dělat forward pass znamená, že předáváme hodnotu z proměnných ve směru vpřed zleva (vstup) doprava, kde je výstup.

uvažujme příklad tím, že dáme nějakou hodnotu všem vstupům. Předpokládejme, že pro všechny vstupy jsou uvedeny následující hodnoty.

$$x=1, y=3, z=-3$$

Tím, že tyto hodnoty vstupů, můžeme provádět dopředu projít a získat následující hodnoty pro výstupy na každém uzlu.

nejprve použijeme hodnotu x = 1 a y = 3, abychom získali p = 4.

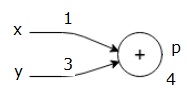
pak použijeme p = 4 a z = -3, abychom získali g = -12. Jdeme zleva doprava, dopředu.

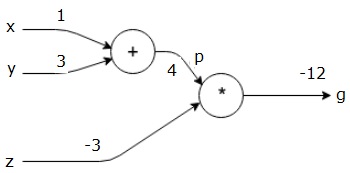
Cíle Dozadu Projít

V zaostalých projít, náš záměr je výpočet gradientů pro každý vstup s ohledem na finální výstup. Tyto přechody jsou nezbytné pro trénink neuronové sítě pomocí gradientního sestupu.

například požadujeme následující přechody.

Požadované gradienty

$$\frac{\partial x}{\partial f}, \frac{\partial y}{\partial f}, \frac{\partial z}{\partial f}$$

Backward pass (backpropagation)

začneme zpětně projít tím, že najde derivace výstupu s ohledem na konečný výstup (sám!). Výsledkem bude odvození identity a hodnota se rovná jedné.

$$\frac{\partial g}{\partial g} = 1$$

Naše výpočetní graf teď vypadá, jak je uvedeno níže −

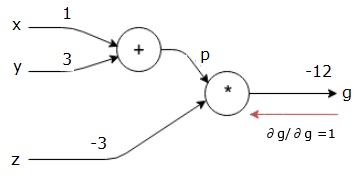
Next, budeme dělat dozadu projít “*” operace. Budeme počítat přechody na p a z. Protože g = p*z, víme, že−

$$\frac{\partial g}{\partial z} = p$$

$$\frac{\partial g}{\partial p} = z$$

už známe hodnoty z a p z přihrávky dopředu. Proto jsme si−

$$\frac{\partial g}{\partial z} = p = 4$$

a

$$\frac{\partial g}{\partial p} = z = -3$$

chceme k výpočtu gradientů na x a y−

$$\frac{\partial g}{\partial x}, \frac{\partial g}{\partial y}$$

Nicméně, chceme to udělat efektivně (i když x a g jsou pouze dvě zastávky dál v tomto grafu, představte si, že je opravdu daleko od sebe). Pro efektivní výpočet těchto hodnot použijeme řetězové pravidlo diferenciace. Z řetězce pravidlo, máme−

$$\frac{\partial g}{\partial x}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial x}$$

$$\frac{\partial g}{\partial y}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial y}$$

Ale my už víme, gř/dp = -3, dp/dx a dp/dy jsou snadné, protože p je přímo závislá na x a y. Máme −

$$p=x+y\Rightarrow \frac{\partial x}{\partial p} = 1, \frac{\partial y}{\partial p} = 1$$

Proto jsme si−

$$\frac{\partial g} {\partial f} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial x} = \left ( -3 \right ).1 = -3$$

kromě toho, pro vstup y−

$$\frac{\partial g} {\partial y} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial y} = \left ( -3 \right ).1 = -3$$

hlavním důvodem pro to zpět je to, že když jsme museli vypočítat gradient na x, použili jsme pouze již vypočtené hodnoty a dq/dx (derivace výstupu uzlu s ohledem na vstup stejného uzlu). Použili jsme místní informace k výpočtu globální hodnoty.

Kroky pro trénink neuronové sítě

Postupujte podle těchto kroků k vlaku neuronové sítě−

• Pro datový bod x v dataset,jsme vpřed projít x jako vstup, a výpočet nákladů c jako výstupní.

• děláme zpětný průchod začínající na c, a vypočítat přechody pro všechny uzly v grafu. To zahrnuje uzly, které představují váhy neuronové sítě.

• pak aktualizujeme váhy tím, že děláme přechody W = W – learning rate*.

• tento postup opakujeme, dokud nejsou splněna kritéria zastavení.