Gráficos Computacionales

La backpropagación se implementa en marcos de aprendizaje profundo como Tensorflow, Torch, Theano, etc., mediante el uso de gráficos computacionales. Más significativamente, la comprensión de la propagación inversa en gráficos computacionales combina varios algoritmos diferentes y sus variaciones, como backprop a través del tiempo y backprop con pesos compartidos. Una vez que todo se convierte en un gráfico computacional, siguen siendo el mismo algoritmo, solo la propagación en gráficos computacionales.

Qué es un gráfico Computacional

Un gráfico computacional se define como un gráfico dirigido donde los nodos corresponden a operaciones matemáticas. Los gráficos computacionales son una forma de expresar y evaluar una expresión matemática.

Por ejemplo, aquí hay una ecuación matemática simple –

p p = x + y

Podemos dibujar un gráfico computacional de la ecuación anterior de la siguiente manera.

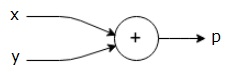
El gráfico computacional anterior tiene un nodo de suma (nodo con signo”+”) con dos variables de entrada x e y y una salida q.

Tomemos otro ejemplo, un poco más complejo. Tenemos la siguiente ecuación.

g g = \ left (x+y \right ) \ast z

La ecuación anterior está representada por el siguiente gráfico computacional.

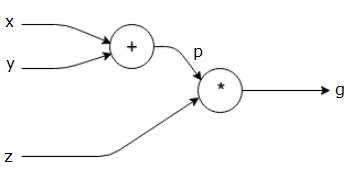
Gráficos computacionales y Backpropagación

Gráficos computacionales y backpropagación, ambos son conceptos centrales importantes en el aprendizaje profundo para el entrenamiento de redes neuronales.

Forward Pass

Forward pass es el procedimiento para evaluar el valor de la expresión matemática representada por gráficos computacionales. Hacer paso hacia adelante significa que estamos pasando el valor de las variables en dirección hacia adelante desde la izquierda (entrada) a la derecha donde está la salida.

Consideremos un ejemplo dando algún valor a todas las entradas. Supongamos que se dan los siguientes valores a todas las entradas.

x x = 1, y=3, z=-3$$

Al dar estos valores a las entradas, podemos realizar un paso hacia adelante y obtener los siguientes valores para las salidas en cada nodo.

Primero, usamos el valor de x = 1 e y = 3, para obtener p = 4.

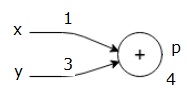
Luego usamos p = 4 y z = -3 para obtener g = -12. Vamos de izquierda a derecha, hacia adelante.

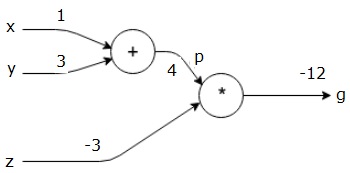
Objetivos de Paso hacia atrás

En el paso hacia atrás, nuestra intención es calcular los gradientes para cada entrada con respecto a la salida final. Estos gradientes son esenciales para entrenar la red neuronal utilizando el descenso de gradiente.

Por ejemplo, deseamos los siguientes degradados.

Deseado gradientes

$$\frac{\partial x}{\partial f}, \frac{\partial y}{\partial f}, \frac{\partial z}{\partial f}$$

pase Atrás (retropropagación)

comenzamos el pase atrás por encontrar la derivada de la salida final con respecto a la salida final (sí!). Por lo tanto, resultará en la derivación de identidad y el valor es igual a uno.

\ \ frac {\partial g} {\partial g} = 1$$

Nuestro gráfico computacional ahora se ve como se muestra a continuación:

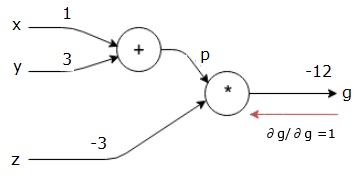
A continuación, haremos el paso hacia atrás a través de la operación”*”. Vamos a calcular los gradientes en p y z. Puesto que g = p*z, sabemos que−

$$\frac{\partial g}{\partial z} = p$$

$$\frac{\partial g}{\partial p} = z$$

ya sabemos que los valores de z y p desde el pase hacia adelante. Por lo tanto, obtenemos−

$$\frac{\partial g}{\partial z} = p = 4$$

y

$$\frac{\partial g}{\partial p} = z = -3$$

queremos calcular los gradientes en x e y−

$$\frac{\partial g}{\partial x}, \frac{\partial g}{\partial y}$$

sin Embargo, queremos hacer esto de manera eficiente (aunque x y g son sólo dos saltos de distancia en este gráfico, imaginar estar muy lejos el uno del otro). Para calcular estos valores de manera eficiente, usaremos la regla de diferenciación de la cadena. A partir de la regla de la cadena, tenemos−

$$\frac{\partial g}{\partial x}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial x}$$

$$\frac{\partial g}{\partial y}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial y}$$

Pero ya sabemos que la dg/dp = -3, dp/dx dp/dy son de fácil puesto que p depende directamente de x y y. Tenemos −

$$p=x+y\Rightarrow \frac{\partial x}{\partial p} = 1, \frac{\partial y}{\partial p} = 1$$

por lo tanto, obtenemos−

$$\frac{\partial g} {\partial f} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial x} = \left ( -3 \derecho ).1 = -3$$

además, para la entrada y−

$$\frac{\partial g} {\partial y} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial y} = \left ( -3 \derecho ).1 = -3$$

La razón principal para hacer esto hacia atrás es que cuando tuvimos que calcular el gradiente en x, solo usamos valores ya calculados y dq / dx (derivada de la salida del nodo con respecto a la entrada del mismo nodo). Utilizamos información local para calcular un valor global.

Pasos para entrenar una red neuronal

Siga estos pasos para entrenar una red neuronal−

• Para el punto de datos x en el conjunto de datos,pasamos hacia adelante con x como entrada y calculamos el costo c como salida.

• Hacemos un paso hacia atrás comenzando en c, y calculamos gradientes para todos los nodos en el gráfico. Esto incluye nodos que representan los pesos de la red neuronal.

• A continuación, actualizamos los pesos haciendo gradientes W = W-tasa de aprendizaje*.

• Repetimos este proceso hasta que se cumplan los criterios de parada.