Laskennalliset graafit

Backpropagation toteutetaan syvissä oppimisympäristöissä, kuten Tensorflow, Torch, Theano jne., käyttämällä laskennallisia kaavioita. Vielä merkittävämpää on ymmärtää takaisin etenemisen laskennallisia kaavioita yhdistää useita eri algoritmeja ja sen muunnelmia, kuten backprop läpi ajan ja backprop jaettujen painojen. Kun kaikki muunnetaan laskennallisen kuvaajan, ne ovat edelleen sama algoritmi-vain takaisin eteneminen laskennallisen kaavioita.

mikä on laskennallinen kuvaaja

laskennallinen kuvaaja määritellään suunnatuksi kuvaajaksi, jossa solmut vastaavat matemaattisia operaatioita. Laskennalliset graafit ovat tapa ilmaista ja arvioida matemaattista lauseketta.

esimerkiksi tässä on yksinkertainen matemaattinen yhtälö –

$$p = x+y$ $

voimme piirtää edellä mainitusta yhtälöstä laskennallisen kuvaajan seuraavasti.

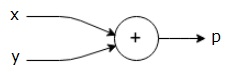
edellä olevassa laskennallisessa kuvaajassa on yhteenlaskusolmu (solmu, jossa on ” + ” – merkki), jossa on kaksi tulomuuttujaa x ja y ja yksi lähtö q.

Otetaanpa toinen esimerkki, hieman monimutkaisempi. Meillä on seuraava yhtälö.

$$g = \left (x+y \right ) \ast z $$

yllä olevaa yhtälöä esittää seuraava laskennallinen kaavio.

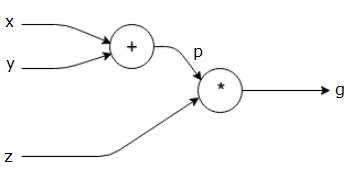
Laskennalliset graafit ja Backpropagaatio

Laskennalliset graafit ja backpropagaatio ovat molemmat tärkeitä ydinkäsitteitä syväoppimisessa neuroverkkojen harjoittelussa.

Forward Pass

Forward pass on menetelmä laskennallisten kuvaajien esittämän matemaattisen lausekkeen arvon arvioimiseksi. Doing forward pass tarkoittaa, että siirrämme arvon muuttujista eteenpäin vasemmalta (tulo) oikealle, jossa lähtö on.

Tarkastellaanpa esimerkkiä antamalla jonkin verran arvoa kaikille panoksille. Oletetaan, seuraavat arvot annetaan kaikille panokset.

$x = 1, y=3, z=-3$$

antamalla nämä arvot tuloa, voimme suorittaa eteenpäin pass ja saada seuraavat arvot lähdöt kunkin solmun.

ensin käytetään arvoa x = 1 ja y = 3, jolloin saadaan P = 4.

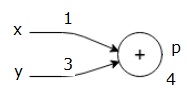
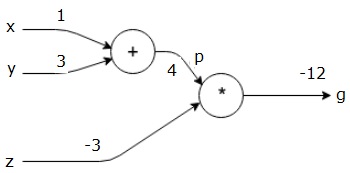
sitten käytetään P = 4 ja z = -3, jotta saadaan g = -12. Menemme vasemmalta oikealle, eteenpäin.

Objectives of Backward Pass

in the backward pass, We intendence is to computing the gradients for each input with respect the final output. Nämä gradientit ovat välttämättömiä neuroverkkojen kouluttamiseksi gradientin laskeutumisen avulla.

esimerkiksi haluamme seuraavat gradientit.

halutut liukuvärit

$$\frac{\partial x}{\partial f}, \frac{\partial y}{\partial f}, \frac{\partial z}{\partial F}$$

taaksepäin pass (backpropagation)

aloitamme taaksepäin menon löytämällä lopputuloksen derivaatan suhteessa lopputulokseen (itse!). Näin ollen se johtaa identiteetin derivointiin ja arvo on yhtä suuri kuin yksi.

$ $ \frac{\partial g}{\partial g}} = 1$$

laskennallinen kuvaajamme näyttää nyt alla esitetyllä tavalla –

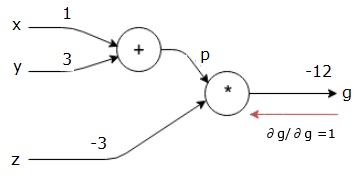
seuraavaksi teemme taaksepäin läpäisyn ” * ” – operaation kautta. Laskemme gradientit P ja z. Koska g = p * z, tiedämme, että−

$$\frac{\partial g}{\partial z} = p$$

$$\frac{\partial g}{\partial p} = z$$

tiedämme jo z: n ja p: n arvot eteenpäin kulkevasta solasta. Siksi saamme−

$$\frac{\partial g}{\partial z} = p = 4$$

ja

$ $ \frac{\partial g}{\partial p} = z = -3$$

haluamme laskea gradientit X ja y−

$$\frac{\partial g} {\partial x},\frac{\partial g} {\partial y}$$

haluamme kuitenkin tehdä tämän tehokkaasti (vaikka x ja g ovat tässä kaaviossa vain kahden humalan päässä, kuvitelkaa niiden olevan todella kaukana toisistaan). Jotta nämä arvot voidaan laskea tehokkaasti, käytämme eriyttämisen ketjusääntöä. Ketjusäännöstä olemme−

$$\frac {\partial g} {\partial x}=\frac{\partial g}{\partial p}\ast \frac{\partial P}{\partial x}$$

$$\frac{\partial g}{\partial y}=\frac{\partial g}{\partial p}\ast \frac {\partial p} {\partial y}$$

mutta tiedämme jo, että DG/dp = -3, dp/dx ja dp / dy ovat helppoja, koska p riippuu suoraan x: stä ja y: stä. Meillä on –

$$p = x + y\Rightarrow \frac{\partial x}{\partial p} = 1, \frac{\partial y} {\partial p}} = 1$$

siksi saamme−

$$\frac{\partial g} {\partial f} = \frac{\partial g} {\partial p}\ast \frac{\partial P} {\partial x} = \left ( -3 \right ).1 = -3$$

lisäksi syötteelle y−

$$\frac{\partial g} {\partial y} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial y} = \left ( -3 \right ).1 = -3$$

tärkein syy tehdä tämä taaksepäin on, että kun meidän piti laskea gradientin X, käytimme vain jo lasketut arvot, ja dq/dx (johdannainen solmun lähtö suhteessa saman solmun tulo). Käytimme paikallista tietoa globaalin arvon laskemiseen.

hermoverkon harjoitteluaskeleet

hermoverkon harjoitteluaskeleet−

• datajoukon data point x: n kohdalla teemme eteenpäin passia x: n ollessa tulona ja laskemme kustannukset c: n tuotoksena.

• teemme taaksepäin kulkea alkaen C, ja laskea gradientit kaikkien solmujen kuvaajan. Tämä sisältää solmut, jotka edustavat neuroverkkopainoja.

• sitten päivitämme painot tekemällä W = W-learning rate * gradientit.

• toistamme tätä prosessia, kunnes stop-kriteerit täyttyvät.