Graphiques Computationnels

La rétropropagation est implémentée dans des frameworks d’apprentissage en profondeur tels que Tensorflow, Torch, Theano, etc., en utilisant des graphiques de calcul. De manière plus significative, la compréhension de la propagation arrière sur les graphes de calcul combine plusieurs algorithmes différents et ses variations telles que backprop dans le temps et backprop avec des poids partagés. Une fois que tout est converti en graphe de calcul, ils sont toujours le même algorithme − il suffit de revenir sur la propagation sur les graphes de calcul.

Qu’est-ce qu’un Graphe de calcul

Un graphe de calcul est défini comme un graphe dirigé où les nœuds correspondent à des opérations mathématiques. Les graphes computationnels sont un moyen d’exprimer et d’évaluer une expression mathématique.

Par exemple, voici une équation mathématique simple –

$$p = x + y

Nous pouvons dessiner un graphique de calcul de l’équation ci-dessus comme suit.

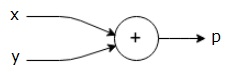
Le graphe computationnel ci-dessus a un nœud d’addition (nœud avec le signe “+”) avec deux variables d’entrée x et y et une sortie q.

Prenons un autre exemple, légèrement plus complexe. Nous avons l’équation suivante.

gg = \left (x + y\right) \ast z $$

L’équation ci-dessus est représentée par le graphique de calcul suivant.

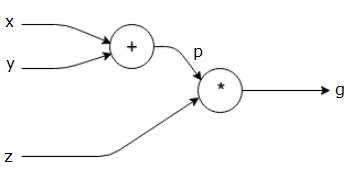
Graphes computationnels et Rétropropagation

Les graphes computationnels et la rétropropagation sont tous deux des concepts de base importants de l’apprentissage en profondeur pour l’entraînement des réseaux de neurones.

Forward Pass

Forward pass est la procédure d’évaluation de la valeur de l’expression mathématique représentée par des graphes de calcul. Faire une passe vers l’avant signifie que nous passons la valeur des variables dans la direction vers l’avant de la gauche (entrée) vers la droite où se trouve la sortie.

Prenons un exemple en donnant une certaine valeur à toutes les entrées. Supposons que les valeurs suivantes soient données à toutes les entrées.

$$x = 1, y = 3, z=-3$$

En donnant ces valeurs aux entrées, nous pouvons effectuer une passe en avant et obtenir les valeurs suivantes pour les sorties sur chaque nœud.

Tout d’abord, nous utilisons la valeur de x = 1 et y = 3, pour obtenir p = 4.

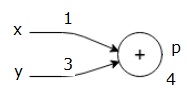
Ensuite, nous utilisons p = 4 et z =-3 pour obtenir g =-12. Nous allons de gauche à droite, en avant.

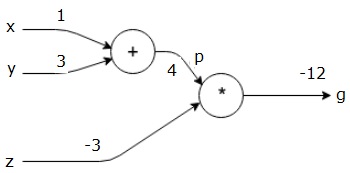
Objectifs de Passage arrière

Dans le passage arrière, notre intention est de calculer les gradients de chaque entrée par rapport à la sortie finale. Ces gradients sont essentiels pour entraîner le réseau de neurones en utilisant la descente de gradient.

Par exemple, nous désirons les dégradés suivants.

Gradients souhaités

\\frac{\partial x}{\partial f}, \frac{\partial y}{\partial f}, \frac{\partial z}{\partial f}

Passage arrière (rétropropagation)

Nous commençons le passage arrière en trouvant la dérivée de la sortie finale par rapport à la sortie finale (elle-même!). Ainsi, cela entraînera la dérivation de l’identité et la valeur est égale à un.

$$\frac {\partial g} {\partial g} = 1$$

Notre graphique de calcul se présente maintenant comme indiqué ci-dessous –

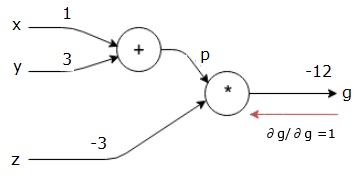
Ensuite, nous effectuerons le passage en arrière à travers l’opération “*”. Nous allons calculer les gradients à p et z. Puisque g = p*z, nous savons que −

$$\ frac {\partial g} {\partial z} = p$$

$$\ frac {\partial g} {\partial p} = z$$

Nous connaissons déjà les valeurs de z et p de la passe avant. Par conséquent, nous obtenons −

$$\ frac {\partial g} {\partial z} = p = 4$$

et

$$\frac {\partial g} {\partial p} = z = -3$$

Nous voulons calculer les gradients à x et y −

$$\ frac {\partial g}{\partial x}, \frac{\partial g}{\partial y}

Cependant, nous voulons le faire efficacement (bien que x et g ne soient qu’à deux sauts dans ce graphique, imaginez-les vraiment éloignés l’un de l’autre). Pour calculer ces valeurs efficacement, nous utiliserons la règle de la chaîne de différenciation. De la règle de la chaîne, nous avons −

$$\ frac {\partial g} {\partial x} = \frac {\partial g}{\partial p}\ast\frac{\partial p}{\partial x}$$

$$\ frac {\partial g}{\partial y} = \frac{\partial g}{\partial p}\ast\frac{\partial p}{\partial y}$$

Mais nous savons déjà que dg/dp =-3, dp/dx et dp/dy sont faciles puisque p dépend directement de x et y. Nous avons −

$$p = x + y \Rightarrow\frac {\partial x}{\partial p} = 1, \frac {\partial y}{\partial p} = 1$$

Par conséquent, nous obtenons −

$$\ frac {\partial g}{\partial f} = \frac {\partial g}{\partial p}\ast\frac{\partial p}{\partial x} = \left (-3\right).1 = -3$$

De plus, pour l’entrée y −

$$\ frac {\partial g}{\partial y} = \frac {\partial g}{\partial p}\ast\frac{\partial p}{\partial y} = \left (-3\right).1 = -3$$

La principale raison de faire cela en arrière est que lorsque nous devions calculer le gradient à x, nous n’utilisions que des valeurs déjà calculées, et dq / dx (dérivée de la sortie du nœud par rapport à l’entrée du même nœud). Nous avons utilisé des informations locales pour calculer une valeur globale.

Étapes d’entraînement d’un réseau de neurones

Suivez ces étapes pour entraîner un réseau de neurones −

• Pour le point de données x dans l’ensemble de données, nous transmettons avec x en entrée et calculons le coût c en sortie.

• Nous passons en arrière à partir de c et calculons les gradients pour tous les nœuds du graphique. Cela inclut les nœuds qui représentent les poids du réseau neuronal.

• Nous mettons ensuite à jour les poids en faisant W = W – taux d’apprentissage * gradients.

• Nous répétons ce processus jusqu’à ce que les critères d’arrêt soient remplis.