Beregnings Grafer

Backpropagation er implementert i dype læringsrammer som Tensorflow, Torch, Theano, etc., ved hjelp av beregnings grafer. Mer signifikant, forståelse tilbake forplantning på beregningsgrafer kombinerer flere forskjellige algoritmer og dens variasjoner som backprop gjennom tid og backprop med delte vekter. Når alt er omgjort til en beregningsgraf, er de fortsatt den samme algoritmen − bare tilbake forplantning på beregningsgrafer.

Hva Er Beregningsgraf

en beregningsgraf er definert som en rettet graf der nodene samsvarer med matematiske operasjoner. Beregningsgrafer er en måte å uttrykke og evaluere et matematisk uttrykk på.

for eksempel er her en enkel matematisk ligning –

$ $ p = x + y$$

vi kan tegne en beregningsgraf av ligningen ovenfor som følger.

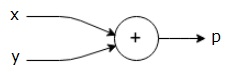
ovennevnte beregnings graf har en addisjon node (node med ” + ” tegn) med to inngangsvariabler x og y og en utgang q.

la oss ta et annet eksempel, litt mer komplekst. Vi har følgende ligning.

$ $ g = \ venstre (x+y \høyre ) \ast z $ $

ovennevnte ligning er representert av følgende beregningsgraf.

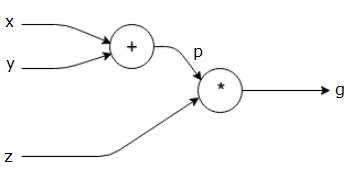
Beregnings Grafer Og Backpropagation

Beregnings grafer og backpropagation, begge er viktige kjernekonsepter i dyp læring for trening nevrale nettverk.

Forward Pass

Forward pass er prosedyren for å evaluere verdien av det matematiske uttrykket representert av beregningsgrafer. Å gjøre fremoverpass betyr at vi overfører verdien fra variabler i fremoverretning fra venstre (inngang) til høyre der utgangen er.

la oss vurdere et eksempel ved å gi noen verdi til alle inngangene. Anta at følgende verdier er gitt til alle inngangene.

$ $ x=1, y = 3, z=-3$$

ved å gi disse verdiene til inngangene, kan vi utføre fremoverpass og få følgende verdier for utgangene på hver node.

først bruker vi verdien av x = 1 og y = 3, for å få p = 4.

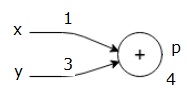
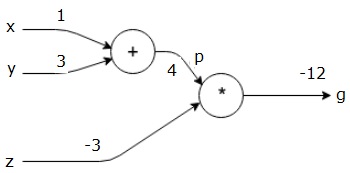
så bruker vi p = 4 og z = -3 for å få g = -12. Vi går fra venstre til høyre, fremover.

Mål For Backward Pass

i backward pass er vår intensjon å beregne gradientene for hver inngang med hensyn til den endelige utgangen. Disse gradienter er avgjørende for trening av nevrale nettverk ved hjelp av gradient nedstigning.

for eksempel ønsker vi følgende gradienter.

Ønskede gradienter

$$\frac{\partial x}{\partial f}, \frac{\partial y}{\partial f}, \frac{\partial z}{\partial f}$$

Bakover pass (backpropagation)

vi starter bakoverpasset ved å finne derivatet av den endelige utgangen med hensyn til den endelige utgangen (selv!). Dermed vil det resultere i identitetsavledning og verdien er lik en.

$$\frac{\delvis g}{\delvis g} = 1$$

vår beregningsgraf ser nå ut som vist nedenfor –

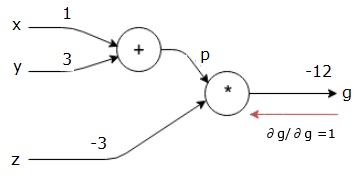
Neste vil vi gjøre bakoverpasset gjennom ” * ” – operasjonen. Vi vil beregne gradientene ved p og z. Siden g = p * z, vet vi det−

$$\frac {\partial g} {\partial z} = p$$

$$\frac {\partial g} {\partial p} = z$$

vi vet allerede verdiene av z og p fra fremoverpasset. Derfor får vi−

$$\frac {\partial g} {\partial z} = p = 4$$

og

$ $ \frac {\delvis g} {\delvis p} = z = -3$$

vi ønsker å beregne gradienter ved x og y−

$$\frac {\partial g} {\partial x}, \frac{\partial g} {\partial y} $ $

vi vil imidlertid gjøre dette effektivt (selv om x og g bare er to hopp unna i denne grafen, tenk at de er veldig langt fra hverandre). For å beregne disse verdiene effektivt, vil vi bruke kjederegelen for differensiering. Fra kjederegelen har vi−

$$\frac {\partial g} {\partial x}=\frac {\partial g} {\partial p}\ast \ frac {\partial p}{\partial x}$$

$$\frac {\partial g} {\partial y}=\frac {\partial g} {\partial p} \ast\frac {\partial p} {\partial y}$$

Men vi vet allerede at dg/dp = -3, dp/dx og dp / dy er enkle siden p direkte avhenger av x og y. Vi har –

$ $ p = x + y \ Rightarrow \frac {\partial x} {\partial p} = 1, \frac {\partial y} {\partial p} = 1$$

Derfor får vi−

$$\frac {\partial g} {\partial f} = \frac{\partial g} {\partial p}\ast \ frac {\partial p} {\partial x} = \venstre ( -3 \ høyre).1 = -3$$

i tillegg, for inngangen y−

$$\frac {\partial g} {\partial y} = \frac{\partial g} {\partial p}\ast \ frac {\partial p} {\partial y} = \venstre (-3 \ høyre).1 = -3$$

hovedårsaken til å gjøre dette bakover er at når vi måtte beregne gradienten ved x, brukte vi bare allerede beregnede verdier,og dq / dx (derivat av nodeutgang med hensyn til samme nodes inngang). Vi brukte lokal informasjon til å beregne en global verdi.

Trinn for å trene et nevralt nettverk

Følg disse trinnene for å trene et nevralt nettverk−

• for datapunkt x i datasett gjør vi fremoverpass med x som inngang, og beregner kostnaden c som utgang.

• vi gjør bakoverpass som starter ved c, og beregner gradienter for alle noder i grafen. Dette inkluderer noder som representerer nevrale nettverksvekter.

• vi oppdaterer deretter vektene ved Å gjøre w = W – learning rate * gradienter.

• vi gjentar denne prosessen til stoppkriteriene er oppfylt.