wykresy komputerowe

Backpropagation jest zaimplementowany w frameworkach deep learning takich jak TensorFlow, Torch, Theano itp., za pomocą wykresów obliczeniowych. Co ważniejsze, zrozumienie propagacji wstecznej na wykresach obliczeniowych łączy kilka różnych algorytmów i ich odmian, takich jak backprop przez czas i backprop ze wspólnymi wagami. Gdy wszystko jest konwertowane na wykres obliczeniowy, są one nadal ten sam algorytm – tylko z powrotem propagacji na wykresach obliczeniowych.

Co to jest Graf obliczeniowy

Graf obliczeniowy jest zdefiniowany jako Graf kierowany, w którym węzły odpowiadają operacjom matematycznym. Wykresy obliczeniowe są sposobem wyrażania i oceny wyrażenia matematycznego.

na przykład, oto proste równanie matematyczne −

$$p = x+y$$

możemy narysować wykres obliczeniowy powyższego równania w następujący sposób.

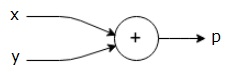
powyższy wykres obliczeniowy ma dodatkowy węzeł (węzeł ze znakiem”+”) z dwiema wejściowymi zmiennymi x i y oraz jedną wyjściową q.

weźmy inny przykład, nieco bardziej złożony. Mamy następujące równanie.

$ $ g = \ left (x+y \right ) \ast z $$

powyższe równanie jest reprezentowane przez następujący wykres obliczeniowy.

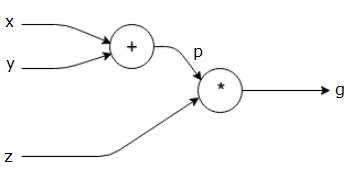
wykresy obliczeniowe i Backpropagacja

wykresy obliczeniowe i backpropagacja, oba są ważnymi podstawowymi pojęciami w głębokim uczeniu do szkolenia sieci neuronowych.

Forward Pass

Forward pass to procedura oceny wartości wyrażenia matematycznego reprezentowanego przez wykresy obliczeniowe. Wykonanie forward pass oznacza, że przekazujemy wartość ze zmiennych w kierunku do przodu od lewej (wejście) do prawej, gdzie jest wyjście.

rozważmy przykład podając pewną wartość wszystkim wejściom. Załóżmy, że następujące wartości są podane dla wszystkich wejść.

$$x=1, y=3, z=-3$$

podając te wartości wejściom, możemy wykonać forward pass i uzyskać następujące wartości dla wyjść na każdym węźle.

najpierw używamy wartości x = 1 i y = 3, aby uzyskać p = 4.

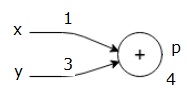
następnie używamy p = 4 i z = -3, aby uzyskać g = -12. Idziemy od lewej do prawej, do przodu.

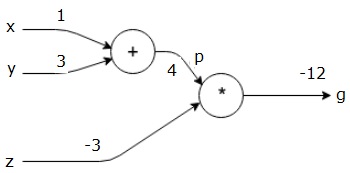
cele przejścia do tyłu

w przejściu do tyłu naszym zamiarem jest obliczenie gradientów dla każdego wejścia w odniesieniu do końcowego wyjścia. Te gradienty są niezbędne do szkolenia sieci neuronowej z wykorzystaniem gradientu zniżania.

na przykład pragniemy następujących gradientów.

pożądane gradienty

$$\frac{\partial x}{\partial f}, \frac{\partial y}{\partial f}, \frac{\partial z}{\partial f}$$

Backward pass (backpropagation)

rozpoczynamy backward pass od znalezienia pochodnej końcowego wyniku względem końcowego wyniku (samego!). W ten sposób spowoduje to wyprowadzenie tożsamości, a wartość jest równa 1.

$$ \ frac {\partial g} {\partial g} = 1$$

nasz wykres obliczeniowy wygląda teraz tak, jak pokazano poniżej –

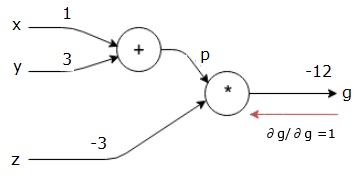
następnie wykonamy backward pass poprzez operację”*”. Obliczymy gradienty w p i z. Ponieważ g = p*z, wiemy, że−

$$\frac {\partial g} {\partial z} = p$$

$$\frac {\partial g} {\partial p} = z$$

znamy już wartości z I p z przejścia do przodu. Stąd otrzymujemy−

$$\frac {\partial g} {\partial z} = p = 4$$

i

$$ \ frac {\partial g} {\partial p} = z = -3$$

chcemy obliczyć gradienty w X i y−

$$\frac {\partial g} {\partial x},\frac {\partial g} {\partial y}$$

jednak chcemy to zrobić efektywnie (chociaż x i g są tylko dwa skoki od siebie na tym wykresie, wyobraź sobie, że są naprawdę daleko od siebie). Aby efektywnie obliczyć te wartości, użyjemy łańcuchowej reguły różnicowania. Z reguły łańcuchowej mamy−

$$\frac {\partial g} {\partial x}= \ frac {\partial g} {\partial P} \ ast \frac {\partial p} {\partial x}$$

$$\frac {\partial g} {\partial y}=\frac{\partial g} {\partial p} \ast\frac{\partial p} {\partial y}$$

ale wiemy już, że dg / dp = -3, dp / dx i dp / dy są łatwe, ponieważ p zależy bezpośrednio od x i y. Mamy –

$$p = x + y\Rightarrow \frac {\partial x} {\partial p} = 1, \frac {\partial y} {\partial p} = 1$$

stąd otrzymujemy−

$$\frac {\partial g} {\partial f} = \ frac {\partial g} {\partial P} \ ast \frac {\partial p} {\partial x} = \ left (-3 \right).1 = -3$$

dodatkowo dla wejścia y−

$$\frac {\partial g} {\partial y} = \ frac {\partial g} {\partial P} \ ast \frac {\partial p} {\partial y} = \ left (-3 \right).1 = -3$$

głównym powodem zrobienia tego wstecz jest to, że kiedy musieliśmy obliczyć gradient w X, użyliśmy tylko już obliczonych wartości i dq / dx (pochodna wyjścia węzła w odniesieniu do tego samego wejścia węzła). Użyliśmy lokalnych informacji do obliczenia globalnej wartości.

kroki treningu sieci neuronowej

wykonaj następujące kroki, aby trenować sieć neuronową−

• dla punktu danych x w zbiorze danych wykonujemy przekazanie do przodu Z X jako wejściem i obliczamy koszt c jako wyjście.

• przechodzimy wstecz zaczynając od c i obliczamy gradienty dla wszystkich węzłów na wykresie. Obejmuje to węzły, które reprezentują wagi sieci neuronowej.

• następnie aktualizujemy wagi, wykonując gradienty W = w-learning rate *.

• powtarzamy ten proces aż do spełnienia kryteriów stop.