Computacionais Gráficos

Backpropagation é implementado em uma aprendizagem mais profunda frameworks como Tensorflow, Tocha, Theano, etc., usando grafos computacionais. Mais significativamente, a compreensão da propagação traseira em grafos computacionais combina vários algoritmos diferentes e suas variações, como backprop através do tempo e backprop com pesos compartilhados. Uma vez que tudo é convertido em um grafo computacional, eles ainda são o mesmo algoritmo − apenas propagação de volta em grafos computacionais.

What is Computational Graph

A computational graph is defined as a directed graph where the nodes corresponds to mathematical operations. Grafos computacionais são uma forma de expressar e avaliar uma expressão matemática.

por exemplo, aqui está uma equação matemática simples –

$p = x+y$

podemos desenhar um grafo computacional da equação acima como segue.

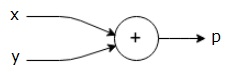
acima computacional gráfico tem um acréscimo de nó (nó com o sinal”+”) com duas variáveis de entrada x e y e uma saída q.

tomemos outro exemplo, um pouco mais complexo. Temos a seguinte equação:

$g = \left (x+y \right ) \ast z $

a equação acima é representada pelo seguinte grafo computacional.

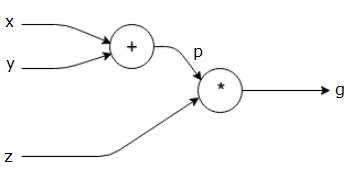
grafos computacionais e Backpropagation

grafos computacionais e backpropagation, ambos são conceitos fundamentais importantes na aprendizagem profunda para a formação de redes neurais.

Forward Pass

Forward pass is the procedure for evaluating the value of the mathematical expression represented by computational graphs. Fazendo a passagem para a frente significa que estamos passando o valor de variáveis na direção para a frente da esquerda (entrada) para a direita onde a saída está.

consideremos um exemplo dando algum valor a todas as entradas. Suponha que os seguintes valores são dados a todas as entradas.

$x = 1, y = 3, z=-3$$

ao dar estes valores para as entradas, podemos realizar passe para a frente e obter os seguintes valores para as saídas em cada nó.

primeiro, usamos o valor de x = 1 e y = 3, para obter p = 4.

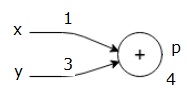
Then we use p = 4 and z = -3 to get g = -12. Vamos da esquerda para a direita, para a frente.

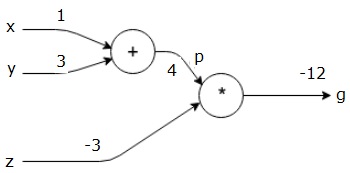
Objectives of Backward Pass

In the backward pass, our intention is to compute the gradients for each input with respect to the final output. Estes gradientes são essenciais para treinar a rede neural usando descida gradiente.

por exemplo, nós desejamos os seguintes gradientes.

Desejado gradientes

$$\frac{\partial x}{\partial f}, \frac{\partial y}{\partial f}, \frac{\partial z}{\partial f}$$

passagem de Retrocesso (backpropagation)

começamos a passagem de retrocesso por encontrar a derivada da saída final com relação ao resultado final (em si!). Assim, resultará na derivação da identidade e o valor é igual a um.

$$\frac {\partial g} {\partial g} = 1$$

nosso grafo computacional agora olha como mostrado abaixo –

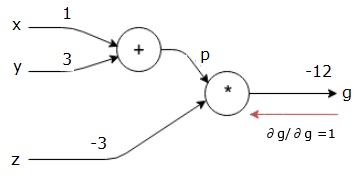
em seguida, vamos fazer o passe para trás através da operação”*”. Vamos calcular os gradientes em p e z. Desde que g = p*z, sabemos que−

$$\frac{\partial g}{\partial z} = p$$

$$\frac{\partial g}{\partial p} = z$$

Nós já sabemos os valores de z e de p a partir de a passar para a frente. Portanto, obtemos−

$$\frac{\partial g}{\partial z} = p = 4$$

e

$$\frac{\partial g}{\partial p} = z = -3$$

queremos calcular os gradientes em x e y−

$$\frac{\partial g}{\partial x}, \frac{\partial g}{\partial y}$$

no Entanto, nós queremos fazer isso de forma eficiente (embora o x e g são apenas dois saltos de distância neste gráfico, imaginar que elas sejam realmente muito próximos um do outro). Para calcular estes valores de forma eficiente, utilizaremos a regra da diferenciação em cadeia. A partir da regra da cadeia, temos−

$$\frac{\partial g}{\partial x}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial x}$$

$$\frac{\partial g}{\partial y}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial y}$$

Mas nós já sabemos que a dg/dp = -3, dp/dx e dp/dy são fáceis uma vez que p depende diretamente de x e y. Temos −

$$p=x+y\Rightarrow \frac{\partial x}{\partial p} = 1, \frac{\partial y}{\partial p} = 1$$

Portanto, obtemos−

$$\frac{\partial g} {\partial f} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial x} = \left ( -3 \right ).1 = -3$$

além disso, para a entrada de y−

$$\frac{\partial g} {\partial y} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial y} = \left ( -3 \right ).1 = -3$$

a principal razão para fazer isso ao contrário é que quando tivemos que calcular o gradiente em x, nós só usamos valores já computados, e dq/dx (derivada da saída do nó com relação à entrada do mesmo nó). Usamos informações locais para calcular um valor global.

Passos para o treinamento de uma rede neural

Siga estes passos para treinar uma rede neural−

• Para dados de ponto de x no conjunto de dados,podemos fazer o passe para a frente com x como entrada e calcular o custo c como saída.

• nós passamos para trás começando em c, e calculamos gradientes para todos os nós no grafo. Isto inclui nós que representam os pesos da rede neural.

• nós então atualizamos os pesos fazendo w = w-taxa de aprendizagem * gradientes.

• repetimos este processo até que os critérios de paragem sejam cumpridos.