számítási grafikonok

a Backpropagation olyan mély tanulási keretekben valósul meg, mint a Tensorflow, Torch, Theano stb., számítási grafikonok használatával. Ennél is fontosabb, hogy a számítási grafikonokon a visszaterjedés megértése több különböző algoritmust és annak variációit ötvözi, mint például a backprop az időben és a backprop a megosztott súlyokkal. Miután mindent átalakítottak számítási gráfmá, továbbra is ugyanaz az algoritmus − csak vissza szaporítás a számítási gráfokon.

mi a számítási gráf

a számítási gráf olyan irányított gráf, ahol a csomópontok matematikai műveleteknek felelnek meg. A számítási gráfok a matematikai kifejezés kifejezésének és értékelésének egyik módja.

például itt van egy egyszerű matematikai egyenlet –

$$p = x+y$$

a fenti egyenlet számítási grafikonját az alábbiak szerint rajzolhatjuk.

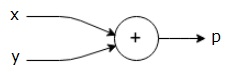
a fenti számítási gráfnak van egy összeadási csomópontja (“+”jelű csomópont) két bemeneti változóval x és y és egy Q kimenettel.

Vegyünk egy másik, kissé összetettebb példát. A következő egyenlet van.

$$g = \left (x+y \right ) \ast z $$

a fenti egyenletet a következő számítási grafikon képviseli.

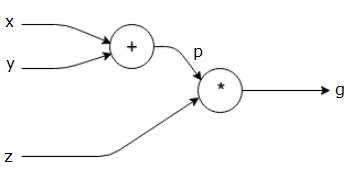
Computational Graph and Backpropagation

Computational graph and backpropagation, mindkettő fontos alapfogalmak a deep learning képzés neurális hálózatok.

Előre lépés

Előre lépés a számítási grafikonok által képviselt matematikai kifejezés értékének értékelésére szolgáló eljárás. Az előre lépés azt jelenti, hogy a változók értékét előre haladjuk balról (bemenet) jobbra, ahol a kimenet van.

tekintsünk egy példát úgy, hogy adunk valamilyen értéket az összes bemenetnek. Tegyük fel, hogy a következő értékeket adjuk meg az összes bemenetnek.

$$x=1, y=3, z=-3$$

azáltal, hogy ezeket az értékeket adjuk meg a bemeneteknek, végrehajthatjuk az előre haladást, és megkaphatjuk a következő értékeket az egyes csomópontokon lévő kimenetekhez.

először x = 1 és y = 3 értékét használjuk, hogy P = 4-et kapjunk.

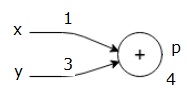
ezután P = 4 és z = -3-at használunk, hogy g = -12-t kapjunk. Balról jobbra megyünk, előre.

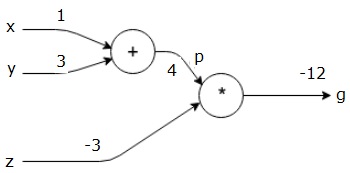
a hátra Pass céljai

a hátra pass-ban szándékunk az, hogy kiszámítsuk az egyes bemenetek gradienseit a végső kimenethez képest. Ezek a gradiensek elengedhetetlenek az ideghálózat gradiens ereszkedéssel történő képzéséhez.

például a következő színátmeneteket kívánjuk.

kívánt színátmenetek

$$ \ FRAC{\részleges x} {\részleges F}, \ frac {\részleges y} {\részleges F},\frac {\részleges z} {\részleges F}$$

visszafelé lépés (backpropagation)

a visszafelé lépést úgy kezdjük, hogy megtaláljuk a végső kimenet deriváltját a végső kimenethez képest (maga!). Így az identitás levezetését eredményezi, és az érték egyenlő egy.

$$ \ frac {\részleges g} {\részleges g} = 1$$

számítási grafikonunk most az alábbiak szerint néz ki –

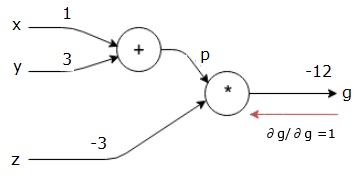
ezután elvégezzük a visszafelé haladást a “*” műveleten keresztül. Mivel g=p * z, tudjuk, hogy−

$$\frac {\parciális g} {\parciális z} = p$$

$$\frac {\partial g}{\partial p} = z$$

már ismerjük a Z és p értékeit a forward pass-ból. Ezért kapunk−

$$\frac {\parciális g} {\parciális z} = p = 4$$

és

$$ \ frac {\részleges g} {\részleges p} = z = -3$$

a gradienseket x-nél és y-nál akarjuk kiszámítani−

$$\frac {\parciális g} {\parciális x}, \ frac {\parciális g} {\parciális y}$$

ezt azonban hatékonyan akarjuk megtenni (bár x és g csak két ugrásra van ebben a gráfban, képzeljük el, hogy nagyon messze vannak egymástól). Ezen értékek hatékony kiszámításához a differenciálás láncszabályát fogjuk használni. Tól lánc szabály, van−

$$\frac {\részleges g} {\részleges x}= \ frac {\részleges g} {\részleges p} \ ast \ frac {\részleges p} {\részleges x}$$

$$\frac {\parciális g} {\parciális y}= \ frac {\parciális g} {\parciális p} \ ast \ frac {\parciális p} {\parciális y}$$

de már tudjuk, hogy a dg/dp = -3, dp/dx és dp/dy könnyű, mivel p közvetlenül függ x-től és y-tól. Van –

$$p=x + y \ Rightarrow \ frac {\részleges x} {\részleges p} = 1, \ frac {\részleges y} {\részleges p} = 1$$

ezért kapunk−

$$\frac {\részleges g} {\részleges F} = \ frac {\részleges g} {\részleges p} \ ast \ frac {\részleges p} {\részleges x} = \ bal ( -3 \ jobb).1 = -3$$

ezenkívül az Y bemenethez−

$$\frac {\részleges g} {\részleges y} = \ frac {\részleges g} {\részleges p} \ ast \ frac {\részleges p} {\részleges y} = \ bal ( -3 \ jobb).1 = -3$$

ennek fő oka visszafelé haladva az, hogy amikor x-nél ki kellett számolnunk a gradienst, csak a már kiszámított értékeket használtuk, valamint a DQ/dx-et (a csomópont kimenetének származéka ugyanazon csomópont bemenetéhez viszonyítva). Helyi információkat használtunk a globális érték kiszámításához.

neurális hálózat kiképzésének lépései

neurális hálózat kiképzéséhez kövesse az alábbi lépéseket−

• az adatkészlet x adatpontjához előre haladunk x bemenettel, és kiszámítjuk a C költséget kimenetként.

• C-től kezdődően visszafelé haladunk, és kiszámítjuk a gráf összes csomópontjának gradienseit. Ez magában foglalja a neurális hálózati súlyokat képviselő csomópontokat is.

• ezután frissítjük a súlyokat W = W – tanulási Arány * színátmenetek elvégzésével.

• ezt a folyamatot addig ismételjük, amíg a stop kritériumok nem teljesülnek.